Question

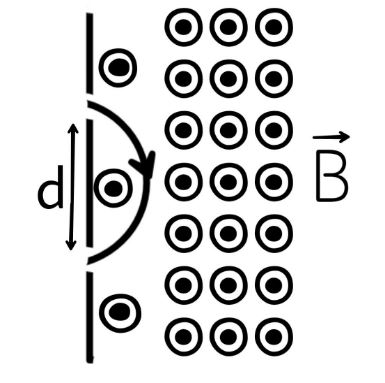
A mass spectrometer is a device which selects particles of equal mass. An iron with electric charge q > 0 starts at rest from a source S and is accelerated through a potential difference V. It passes through a hole into a region of constant magnetic field Vector B perpendicular to the plane of the paper as shown in the figure. The particle is deflected by the magnetic field and emerges through the bottom hole at a distance ‘d’ from the top hole. The mass of the particle

A. $\dfrac{{qBd}}{V}$
B. $\dfrac{{q{B^2}{d^2}}}{{4V}}$
C. $\dfrac{{q{B^2}{d^2}}}{{8V}}$
D. $\dfrac{{qBd}}{{2V}}$

Answer 1

Whenever a body having any given charge irrespective of the mass is accelerated through a potential difference it gains energy, this energy is in the form of kinetic energy which means velocity is associated with the charged moving body.Then if a body is having a charge and velocity moves under a magnetic field it moves in a circular motion If only the magnetic field is perpendicular to the direction of velocity.

Formula used:
The energy of a particle accelerated through a potential difference.
$E = qV$
where $q$ is the charge of the body and $V$ is the potential difference provided.
Kinetic energy:
$KE = \dfrac{1}{2}m{v^2}$
where $v$ is the velocity of the object and $m$ is the mass of the object.
Centripetal force:
$F = \dfrac{{m{v^2}}}{r}$
Where is the mass of the object $v$ is the speed of the object and $r$ is the radius of the circular track in which it is moving.
Force due to magnetic interaction:
$F = qvB$
Where, $q$ is the charge of the body, $v$ is the speed of the body and $B$ is the magnitude of the magnetic field.

Complete step by step answer:
Since the body is accelerated by a potential difference. Thus, the energy of the iron mass $= qV$ where $q$ is the charge of the body and $V$ is the potential difference provided.
Since this energy is stored in the form of kinetic energy as the mass is forced to accelerate
Let the mass of the object be $m$ :
So,
Energy $= qV = \dfrac{1}{2}m{v^2}$where $v$ is the velocity of the mass
${v^2} = \dfrac{{2qV}}{m}$ by rearranging them.
$v = \sqrt {\dfrac{{2qV}}{m}}$
Now the object is passed through an area where the magnetic field is perpendicular to the direction of velocity so it performs a circular motion with diameter $= d$ which mean its radius $= \dfrac{d}{2}$

Since it performs a circular motion, the centripetal force is due to the interaction with magnetic field
$\dfrac{{m{v^2}}}{r} = qvB$
Where is the mass of the object $v$ is the speed of the object and $r$ is the radius of the circular track in which it is moving. $q$ is the charge of the body, $v$ is the speed of the body and $B$ is the magnitude of the magnetic field. Now by substituting the values.
Radius $= \dfrac{d}{2}$ and $v = \sqrt {\dfrac{{2qV}}{m}}$so the equation becomes.
$\dfrac{{m\dfrac{{2qV}}{m}}}{{\dfrac{d}{2}}} = q\sqrt {\dfrac{{2qV}}{m}} B$
$\Rightarrow \dfrac{{4qV}}{d} = qB\sqrt {\dfrac{{2qV}}{m}}$
Now by squaring both the sides
$\dfrac{{16{q^2}{V^2}}}{{{d^2}}} = {q^2}{B^2}\dfrac{{2qV}}{m}$
Now let’s make the mass $m$ the subject of the equation
$m = \dfrac{{2{q^3}{B^2}V{d^2}}}{{16{q^2}{V^2}}} \\\ \Rightarrow m = \dfrac{{q{B^2}{d^2}}}{{8V}}$
Thus, the mass of the object $= \dfrac{{q{B^2}{d^2}}}{{8V}}$

So, the correct answer is option C.

Note: In this question we are assuming the force of friction to be zero and there is no energy loss. But if friction force is encountered then the velocity of the charged mass will decrease, which will make the force due to magnetic field interaction to decrease. If the centripetal force on the charge mass and the speed of the charge mass decreases at the same time this will lead to the decrease in the radius of the circle of rotation in the spectrometer.