Question
Question: A mass of 6 kg is suspended by a rope of length 2 m from the ceiling A force of 50 N in the horizont...
A mass of 6 kg is suspended by a rope of length 2 m from the ceiling A force of 50 N in the horizontal direction is applied at the mid - point P of the rope as shown. What is the angle the rope makes with the vertical in equilibrium?
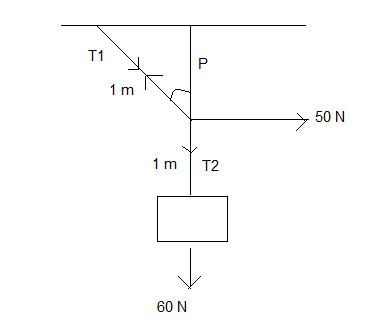
Solution
The force of 50 N acts at the middle of the rope and the block weight acts in the downward direction. Since, the body is in equilibrium so the net force acting on the system is zero. We can use the vector algebra, balancing the forces to find out the solution.
Complete step by step answer:
At point P there are forces acting. The angle made is θ. The tension can be resolved into its components. We can see that weight is balanced by the tension, T2.
∴T2=60N
But the weight is balanced by the horizontal component of the tension, T1.
⇒T1cosθ=T2=60N
The component T1cos θ balances the weight while the component T1sin θ balances the force of 50 N.
So we can write all the questions as:
T1sinθ=50N--(1)
⇒T1cosθ=60N--(2)
Dividing eq (1) by eq (2) we get,
\tan \theta =\dfrac{5}{6} \\\
\Rightarrow \theta ={{\tan }^{-1}}(5/6) \\\
Using an inverse mathematical calculator, we find the value of angle to be 400
Note:
we should always keep in mind that force is a vector quantity and if we have to add two or more than two forces then we have to keep in mind the direction too. Here the forces are either acting in horizontal or either in vertical. If two forces act in opposite directions then resultant can be obtained by subtracting them directly.
