Question
Question: A mass of 2kg is suspended from a steel wire of length 1m and cross-sectional area \[{10^{ - 6}}\,{\...
A mass of 2kg is suspended from a steel wire of length 1m and cross-sectional area 10−6meter2 to form a pendulum arrangement. If the mass is moved to one side and released from the horizontal position of wire then find the maximum extension in the length of the wire.
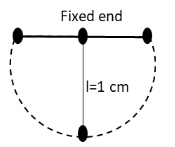
Solution
Use the formula for Young’s modulus for the material of an object. Calculate the force acting on the mass suspended by the steel wire which is the weight of the mass and centripetal force acting on this mass suspended. Use the value of the Young’s modulus for the steel. Substitute all the values in the formula and calculate the extension of the steel wire.
Formulae used:
The Young’s modulus Y for the material of an object is given by
Y=AΔLFL …… (1)
Here, F is the force acting on the object, L is the original length of the object, A is the cross sectional area of the object and ΔL is the change in length of the object.
The centripetal force FC acting on an object is
FC=Rmv2 …… (2)
Here, m is the mass of the object, v is the velocity of the object and R is the radius of the circular path.
Complete step by step solution:
We have given that the mass of 2kg suspended from the steel wire is and the length of the steel wire is 1m.
m=2kg
L=1m
The cross-sectional area of the steel wire is 10−6m2.
A=10−6m2
The Young’s modulus for the steel material is 2×1011N⋅m2.
Y=2×1011N⋅m2
We have asked to calculate the extension in the length of the steel wire.
The weight of the mass suspended is given by
W=mg
Substitute 2kg for m and 10m/s2 for g in the above equation.
W=(2kg)(10m/s2)
⇒W=20N
Hence, the weight of the mass suspended is 20N.
The centripetal force acting on the suspended mass is given by
FC=lmv2
Substitute 2gl for v in the above equation.
FC=lm(2gl)2
⇒FC=2mg
Substitute 20N for mg in the above equation.
⇒FC=2(20N)
⇒FC=40N
The force acting on the steel wire is the sum of weight of the mass suspended and centripetal force acting on the suspended mass.
F=W+FC
Let us calculate the extension in the steel wire.
Substitute W+FC for F in equation (1).
Y=AΔL(W+FC)L
Rearrange the above equation for ΔL.
ΔL=AYWL
Substitute 20N for W, 40N for FC, 1m for L, 10−6m2 for A and 2×1011N⋅m2 for Y in the above equation.
ΔL=(10−6m2)(2×1011N⋅m2)(20N+40N)(1m)
⇒ΔL=3×10−4m
∴ΔL=0.3mm
Hence, the extension in the length of the steel wire is 0.3mm.
Note: The students should keep in mind that the force acting on the mass is not only the weight of the mass. Since the mass attached to the steel wire performs circular motion about its mean position. Hence, the net force acting on this mass is the sum of weight of the mass and centripetal force acting on the mass.
