Solveeit Logo
Login

Question

Question: A mass of \(2kg\) falls from a height of \(40cm\) on a spring of force constant \(1960N{{m}^{-1}}\)....

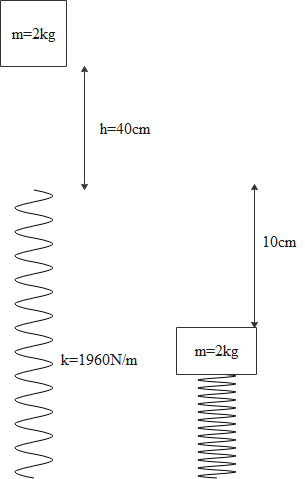
A mass of 2kg2kg falls from a height of 40cm40cm on a spring of force constant 1960Nm−11960N{{m}^{-1}}. The spring is compressed by a value of,
A.10cm B.0.4cm C.0.01cm D.0.04cm \begin{aligned} & A.10cm \\\ & B.0.4cm \\\ & C.0.01cm \\\ & D.0.04cm \\\ \end{aligned}

Explanation

Solution

The gain in the elastic potential energy of the string will be equal to the loss in gravitational potential energy of falling mass. The elastic potential energy is given by the half of the product of force constant and the square of the distance to which spring compressed. And the gravitational potential energy is given as the product of the mass, acceleration due to gravity and the total distance of the travel of the mass. These all may help you to solve this question.

Complete step by step answer:
The terms mentioned in the questions are,
Mass of the particle falling down,
m=2kgm=2kg
Height of the fall is given as,
h=40cmh=40cm
And the force constant is given as,
k=1960Nm−1k=1960N{{m}^{-1}}
Let us assume that the distance to which the spring gets compressed is expressed as xx. Therefore the gain in the elastic potential energy of the string will be equal to the loss in gravitational potential energy of falling mass. This can be written in mathematical way as,
12kx2=mg(h+x)\dfrac{1}{2}k{{x}^{2}}=mg\left( h+x \right)
Where ggbe the acceleration due to gravity which is given as,
g=9.8ms−2g=9.8m{{s}^{-2}}
And the height in metres is,
h=0.4mh=0.4m
Substituting the values in it will give,
12×1960×x2=2×9.8(0.4+x)\dfrac{1}{2}\times 1960\times {{x}^{2}}=2\times 9.8\left( 0.4+x \right)
Simplifying the equation will give,
980x2=7.84+19.6x980{{x}^{2}}=7.84+19.6x
This can be written in the form of a quadratic equation as,
980x2−19.6x−7.84=0980{{x}^{2}}-19.6x-7.84=0
Therefore the value of the distance to which the spring is compressed will be,
19.6±(19.6)2−4×980×−7.842×980=x\dfrac{19.6\pm \sqrt{{{\left( 19.6 \right)}^{2}}-4\times 980\times -7.84}}{2\times 980}=x
Simplifying this equation will give,
x=10cmx=10cm
Therefore the correct answer is obtained. This is given as the option A.

Note:
The force provided by a spring on bodies fixed to its ends is proportional to the spring's variation in length away from its equilibrium length and this will always be directed towards its equilibrium position. The proportionality constant in this relation is known as the spring constant. It gives the amount of the spring's stiffness.