Question

A mass of 100 g strikes the wall with speed 5 m/s at an angle as shown in the figure and it rebounds with the same speed. If the contact time is $2\times 10^{-3}\ sec$, what is the force applied on the mass by the wall?

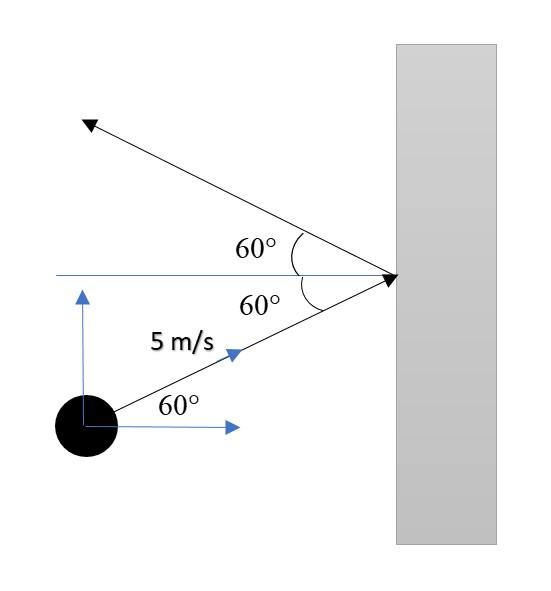
$\text{A.}\quad 250\sqrt3\ N$ to the right.
$\text{B.}\quad 250\ N$ to the right.
$\text{C.}\quad 250\sqrt3\ N$ to the left.
$\text{D.}\quad 250\ N$ to the left.

Answer 1

According to Newton’s second law of motion, force on a body is equal to the rate of change of its momentum. In other words, if there will be a change in momentum of the body, then there must be a force acting on it.

Formula used:
$\vec F = \dfrac{d{\vec P}}{dt}$

Complete step-by-step answer:
In the statement, it is given that the speed of the body after striking the wall is the same as before. The best way to tackle these types of questions is that we can make the free body diagram of the body both before and after the collision and observe the change in velocity in different directions.

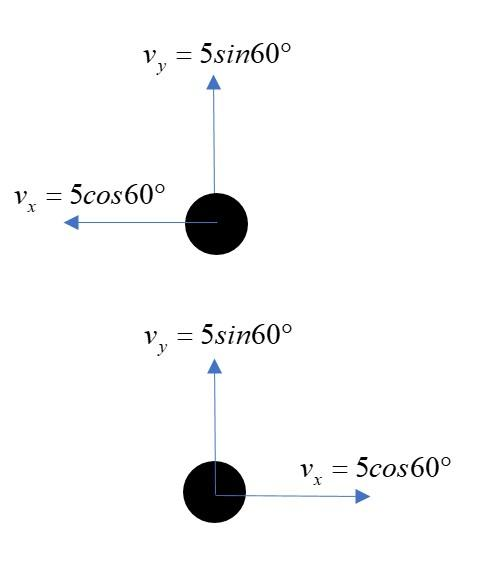
As shown in the above figure, the velocity of the ball in upward direction (Parallel to the wall) is $v_y = 5sin 60^\circ = 5\times \dfrac{\sqrt 3}{2} m/s$. This velocity is constant before and after collision. Thus the force in net direction must be zero, otherwise there must be a change in this velocity (either in magnitude or direction or both).
Now, velocity in x-direction (towards the wall) is $5cos60^\circ = 5\times \dfrac 12 = \dfrac 52 m/s$
But after striking the wall, it changes to $-5cos60^\circ = -\dfrac52 m/s$
Thus change in momentum in x-direction = $m(\dfrac 52 - (-\dfrac 52)) = m\times 5 = 0.1 \times 5 = 0.5 N-s$.
Or $d\vec P = 0.5 Ns$
Also, the time of contact = $dt = 2\times 10^{-3}s$
Hence using:
$\vec F = \dfrac{d{\vec P}}{dt}$
We get $\vec F = \dfrac{0.5}{2\times 10^{-3}} = 250 N$
Now, for the direction, we can say that the force must be applied on the mass towards the left (perpendicular to the wall).

So, the correct answer is “Option D”.

Note: There is one more concept, which is basically the extension of Newton’s second law, which is called the Impulse momentum theorem. We can apply this theorem also to find the force. This is applicable when there is a huge force on a body which acts on a body for a very short period of time.