Solveeit Logo
Login

Question

Question: A mass of 1 kg is suspended by means of a thread. The system is (i) lifted up with an acceleration o...

A mass of 1 kg is suspended by means of a thread. The system is (i) lifted up with an acceleration of 4.9ms−14.9m{{s}^{-1}} (ii) lowered with an acceleration of 4.9ms−24.9m{{s}^{-2}}. The ratio of tension in the first and second case
A. 3:13:1
B. 1:21:2
C. 1:31:3
D. 2:12:1

Explanation

Solution

Use the concept of free body diagram for balancing the force.
Use the application of the second law of newton.
Use the acceleration of gravity in all calculations.

Complete step by step solution:
Students have a clear understanding about free body diagrams and Newton’s Law of Motion.
Newton’s second law is a quantitative description of the changes that a force can produce on the motion of a body. It states that the time rate of change of the momentum of a body is equal in both magnitude and direction to the force imposed on it. The momentum of a body is equal to the product of its mass and its velocity. Momentum, like velocity, is a vector quantity, having both magnitude and direction. A force applied to a body can change the magnitude of the momentum, or its direction, or both. Newton’s second law is one of the most important in all of physics. For a body whose mass m is constant, it can be written in the form F=ma.F=ma. where FF (force) and aa (acceleration) are both vector quantities. If a body has net force acting on it, it is accelerated in accordance with the equation. Conversely, if a body is not accelerated, there is no net force acting on it.

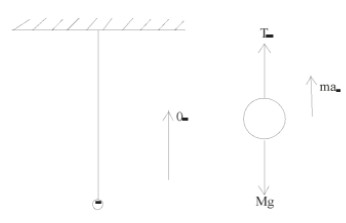
Case (I)
In this case man is lifted up with acceleration 4.9ms−2.4.9m{{s}^{-2}}.
So with the free body diagram
T1−mg=m  a1{{T}_{1}}-mg=m\,\,{{a}_{1}}
T1=m(g+a1){{T}_{1}}=m\left( g+{{a}_{1}} \right)
=1(10+4.9)=14.9  N=1\left( 10+4.9 \right)=14.9\,\,N

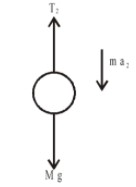
Case (II)
In this case man is moving down with an acceleration 4.9ms−2.4.9m{{s}^{-2}}.
So with the free body diagram:
mg−T2=ma2mg-{{T}_{2}}=m{{a}_{2}}
T2=m(g−a2){{T}_{2}}=m(g-{{a}_{2}})
=(10−4.9)=(10-4.9)
=5.1  N=5.1\ \ N
Ratio: T1T2=14.95.1\dfrac{{{T}_{1}}}{{{T}_{2}}}=\dfrac{14.9}{5.1}
=2.92:1=2.92:1
≃3:1\simeq 3:1
Hence, Option (A) is the correct answer.

Note: Student has clear understanding about free body diagrams.
Students also know how to apply Newton Law of motion.