Question

A mass M of 100 kg is suspended with use of strings A, B and C as shown in figure, where W is vertical wall and R is a rigid horizontal rod. The tension in string B is:

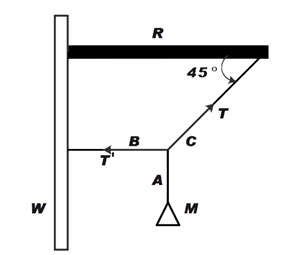
A. 100 gN
B. 0
C. $100\sqrt{2}gN$
D. $\dfrac{100}{\sqrt{2}gN}$

Answer 1

In this question we have been asked to calculate the tension in the string B from the diagram given. It is given that a mass of 100 kg is suspended from the string A. To solve this question, we shall first draw a suitable free body diagram. We shall then calculate the tension in the given string by using the equation of motion from Newton's seconds law for the given system.

Complete Step by step solution:
It is given that 100 kg mass is suspended from a string A.
Now, consider the Free Body diagram below.

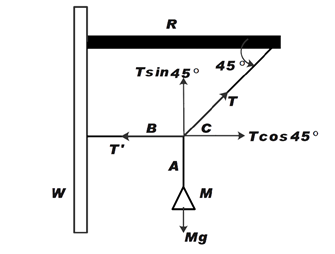
Now, from the diagram we can say that tension in the string B is T’.
Therefore, to calculate T’
After resolving the tension T in string C as shown in the diagram
We get,
$T'=T\cos 45{}^\circ$ …………….. (1)
Using equation of motion from Newton's second law
$Mg=T\sin 45{}^\circ$……………… (2)
Now, the mass is given to be 100 kg.
Also, the options provided to us have used acceleration due to gravity as g therefore, we shall not substitute any value.
Therefore,
$100g=T\dfrac{1}{\sqrt{2}}$
Solving for T
We get,
$T=100\sqrt{2}g$ …………….. (3)
Now from (1) and (3)
We get,
$T'=100\sqrt{2}g\dfrac{1}{\sqrt{2}}$
Therefore,
$T'=100g$ N

Therefore, the correct answer is option A.

Note:
Newton’s second law states that greater the mass of the object, the more force it will require to accelerate. The second law can also be stated as the acceleration of a particle is directly proportional to the force applied on the particle and inversely proportional to the mass of the particle.