Question

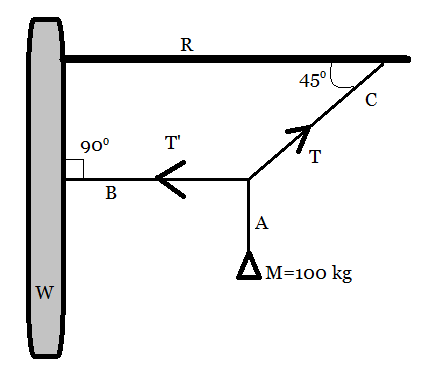
A mass $M$ of $100\;kg$ is suspended with the use of strings $A$, $B$ and $C$ as shown in the figure, where $W$ is a vertical wall and $R$ is a rigid horizontal rod. The tension in string $B$ is:

A. $100\;gN$
B. $0$
C. $100\sqrt 2 \;gN$
D. $\dfrac{{100}}{{\sqrt 2 }}\;gN$

Answer 1

Here we have to resolve the forces so that all forces are along the horizontal and vertical axis only. Thus we see that the tension force on the string $C$, i.e. $T$ needs to be broken into its respective components. Next, we shall equalize the horizontal component of the forces with the vertical component of the forces at the meeting point of the strings since this point is at rest and thus net forces must nullify.

Complete step by step answer:
It is given that the mass is suspended using strings whose tensions are indicated in the diagram. The same diagram has been redrawn with the tension on the string $C$ having been resolved into its horizontal and vertical components.
To do this we have used the parallelogram approach of resolution of vectors into their components. Next, we calculate the angle of the vertical component of the vector with the string $C$ using basic standard methods. The angle thus obtained has been shown separately in the new diagram as ${45^\circ }$ with the vertical axis.

Now we shall equate the horizontal and vertical forces at the point where all the three strings meet. The net tension in the string $B$ is $T'\;$ and the net tension in the string $C$ is $T$ which has been resolved.
The force exerted on the string $A$ is equal to the weight of the mass $M = 40\;kg$. This force is obtained by using Newton’s second law of motion equation, i.e. $f = ma$, where $f$ is the force on a body, $m$ is the mass of the body, and $a$ is the acceleration of the body. Applying this equation on the mass $M$, we have the force $F$ on the string $A$ as $F = Mg$, where $g$ is the acceleration due to gravity. This has been indicated in the diagram.
This is also equal to the vertical force which is acting downwards at the point of intersection of the strings. This downward force is balanced by the vertically upward force of tension, i.e. $T\cos {45^\circ }$.
Thus, equalizing forces on the vertical axis, we have
$T\cos {45^\circ } = Mg$.
$\Rightarrow T\dfrac{1}{{\sqrt 2 }} = Mg$
$\Rightarrow T = Mg\sqrt 2$
Now similarly equalizing forces on the horizontal axis at the meeting point of the strings, we get,
$T' = T\sin {45^\circ }$
Substituting the value of $T$ in this equation, we get,
$T' = (Mg\sqrt 2 )\sin {45^\circ }$
$\Rightarrow T' = (Mg\sqrt 2 )\dfrac{1}{{\sqrt 2 }}$
$\Rightarrow T' = Mg$
Substituting the value of $M = 100\;kg$ in the above equation, we have the tension in S.I. units as,
$\Rightarrow T' = 100g\;N$
This is the value of the tension in the string $B$.
Thus, the correct answer is option (A).

Note: The strings are assumed to be massless as usual since otherwise the mass distribution of the strings would give rise to other forces and the strings would then not form straight lines but instead form a catenary.