Question

A mass $m$ moving with a velocity $v$ collides inelastically with another identical mass at rest. After the collision, the first mass moves with velocity $\dfrac{v}{{\sqrt 3 }}$ in a direction perpendicular to the initial direction of the motion. Find the speed of the second mass after the collision.

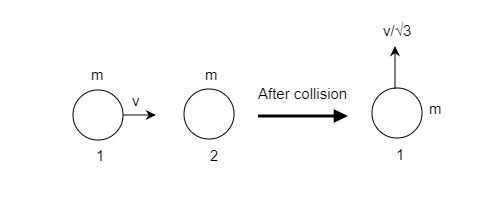
A) $v$
B) $\sqrt 3 v$
C) $\dfrac{{2v}}{{\sqrt 3 }}$
D) $\dfrac{v}{{\sqrt 3 }}$

Answer 1

The first mass is said to move in a direction perpendicular to its initial direction of motion after the collision. Correspondingly the velocity of the second mass will make some angle with the horizontal direction. Here, no external forces are acting on the system and hence the linear momentum is conserved for the collision.

Formula used:
-The linear momentum of a system comprising two masses ${m_1}$ and ${m_2}$ is given by, $p = {m_1}{v_1} + {m_2}{v_2}$ where ${v_1}$ and ${v_2}$ are the velocities of the first mass and the second mass respectively.

Complete step by step answer.
Step 1: Sketch a figure depicting the system before the collision and find the linear momentum of the system before the collision.
The figure represents the system before the collision

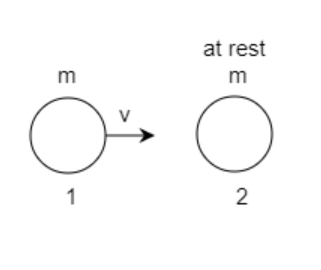
The above figure depicts the first mass moving with velocity ${v_{1x}} = v$ approaching the second mass which is at rest i.e., ${v_{2x}} = 0$ and ${v_{2y}} = 0$. Both the masses are identical i.e., ${m_1} = {m_2} = m$.
The velocity of the first mass is along the x-direction and has no y-component i.e.,${v_{1y}} = 0$ .
Then linear momentum of the above system before the collision in the x-direction will be ${p_{bx}} = m{v_{1x}} + m{v_{2x}}$ ------------ (A)
Substituting values for ${v_{1x}} = v$ and ${v_{2x}} = 0$ in equation (A) we get, ${p_{bx}} = m{v_{1x}} + m{v_{2x}} = mv + 0$
or, ${p_{bx}} = mv$ ----------(1)
The linear momentum of the above system before the collision in the y-direction will be ${p_{by}} = m{v_{1y}} + m{v_{2y}}$ ----------- (B)
Substituting values for ${v_{1y}} = 0$ and ${v_{2y}} = 0$ in equation (B) we get, ${p_{by}} = 0$ ----------(2)
Step 2: Sketch a figure depicting the system after the collision and find the linear momentum of the system after the collision.

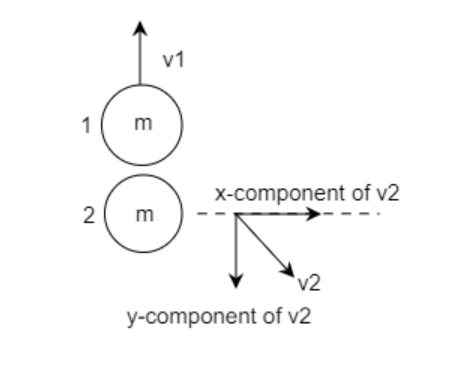
The figure represents the system after the collision

The above figure resolves the velocity ${v_2}$ of the second mass into its x-component ${v_{2x}}$ and its y-component ${v_{2y}}$. The velocity of the first mass ${v_1}$ is along the y-direction and given to be ${v_{1y}} = \dfrac{v}{{\sqrt 3 }}$ and has no x-component i.e., ${v_{1x}} = 0$ .
Then linear momentum of the above system after the collision along the x-direction will be ${p_{ax}} = m{v_{1x}} + m{v_{2x}}$ ---------- (C)
Substituting values for ${v_{1x}} = 0$ in equation (C) we get, ${p_{ax}} = m{v_{2x}}$ ------------- (3)
Similarly, the linear momentum of the above system after the collision along the y-direction will be ${p_{ay}} = m{v_{1y}} + m{v_{2y}}$ ---------- (D)
Substituting values for ${v_{1y}} = \dfrac{v}{{\sqrt 3 }}$ in equation (D) we get, ${p_{ay}} = m\dfrac{v}{{\sqrt 3 }} - m{v_{2y}}$ ---------(4)
Step 3: Use the linear momentum conservation theorem to find the velocity of the second mass.
Here, the momentum of the system before and after the collision along both x and y directions must remain constant.
Thus we can equate equations (1) and (3) for the conservation of momentum along the x-direction.
We then have, $m{v_{2x}} = mv$
Cancelling similar terms on both sides of the above equation we get, ${v_{2x}} = v$
i.e., the x-component of the velocity of the second mass is ${v_{2x}} = v$ .
Similarly, we equate (2) and (4) for the conservation of momentum along the y-direction.
We then have, $0 = m\dfrac{v}{{\sqrt 3 }} - m{v_{2y}}$
Simplifying we get, $\dfrac{v}{{\sqrt 3 }} = {v_{2y}}$
i.e., the y-component of the velocity of the second mass is ${v_{2y}} = \dfrac{v}{{\sqrt 3 }}$ .
Now the resultant velocity ${v_2}$ will be ${v_2} = \sqrt {v_{2x}^2 + v_{2y}^2}$
Substituting values for ${v_{2x}} = v$ and ${v_{2y}} = \dfrac{v}{{\sqrt 3 }}$ in the above expression we get, ${v_2} = \sqrt {{v^2} + {{\left( {\dfrac{v}{{\sqrt 3 }}} \right)}^2}}$
Calculating the square root we get, ${v_2} = \sqrt {{v^2} + \dfrac{{{v^2}}}{3}} = \sqrt {\dfrac{{4{v^2}}}{3}} = \dfrac{{2v}}{{\sqrt 3 }}$
Thus the speed of the second mass is ${v_2} = \dfrac{{2v}}{{\sqrt 3 }}$ .

So the correct option is C.

Note: In equation (4), the momentum of the second mass has a negative sign ( $- m{v_{2y}}$ ). This is because the velocity component of the second mass ${v_{2y}}$ is directed opposite to the velocity component of the first mass ${v_{1y}}$. The initial direction of motion is along the x-direction.