Question

A mass M moving with a certain speed V collides elastically with another stationary mass m. after the collision the masses M and m move with speeds V’ and v respectively. All motion is in one dimension. Then:
$A.\,V=V'+v$
$B.\,V'=V+v$
$C.\,V'={(V+v)}/{2}\;$
$D.\,v=V+V'$

Answer 1

The combination of the law of conservation of momentum along with the law of conservation of energy should be used to solve this type of problem, as the collision gave is a particularly elastic collision.
Formulae used:
${{m}_{1}}({{v}_{1}}-{{u}_{1}})={{m}_{2}}({{v}_{2}}-{{u}_{2}})$
$K{{E}_{i}}+P{{E}_{i}}=K{{E}_{f}}+P{{E}_{f}}$

Complete answer:
From given, we have the data,
The masses = M, m
The velocity of mass M before collision = V
The velocity of mass m before collision = 0
The velocity of mass M after collision = V’
The velocity of mass m after collision = v
The diagram representing before and after the collision of masses.

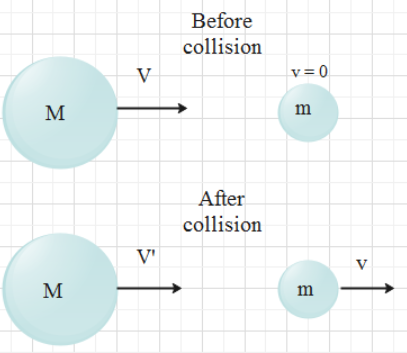
The conservation of momentum states that the amount of momentum remains constant within the isolated system.
When no external force acts on the system, the total momentum before the collision will be equal to the total momentum after the collision.
${{m}_{1}}({{v}_{1}}-{{u}_{1}})={{m}_{2}}({{v}_{2}}-{{u}_{2}})$
where m represents the masses of the respective objects/bodies, v represents the final velocities of the objects/bodies and u represents the initial velocities of the objects/bodies.
In this given scenario, the equation can be represented as,
$MV=MV'+mv$ …… (1)
The second term in the LHS part will be zero, as the mass m was at rest.
The conservation of energy states that the total energy of an isolated system is conserved or remains constant.
The sum of kinetic energy and the potential energy before the collision will be equal to the sum of kinetic energy and the potential energy after the collision.
$K{{E}_{i}}+P{{E}_{i}}=K{{E}_{f}}+P{{E}_{f}}$
Where KE represents the kinetic energy of objects/bodies and PE represents the potential energies.
In this given scenario, the equation can be represented as,
$\dfrac{1}{2}M{{V}^{2}}=\dfrac{1}{2}MV{{'}^{2}}+\dfrac{1}{2}m{{v}^{2}}$ …… (2)
The second term in the LHS part will be zero, as the mass m was at rest.
Combine the equations and solve.
$V=V'+\dfrac{m}{M}v$
From equation (2), we get,

& \dfrac{{{V}^{2}}}{2}=\dfrac{V{{'}^{2}}}{2}+\dfrac{1}{2}\dfrac{m}{M}{{v}^{2}} \\\ & \Rightarrow \dfrac{m}{M}=\dfrac{{{V}^{2}}-V{{'}^{2}}}{{{v}^{2}}} \\\ \end{aligned}$$ Now express the equation in terms of the velocity. $$\begin{aligned} & V=\dfrac{V'v+({{V}^{2}}-V{{'}^{2}})}{v} \\\ & \Rightarrow Vv=V'v=(V+V')(V-V') \\\ & \Rightarrow v=V+V' \\\ \end{aligned}$$ **As the expression obtained is $$v=V+V'$$, thus, the option (D) is correct.** **Additional information:** The elastic collision is a type of collision in which both the momentum and the kinetic energy remains the same or conserved. In other words, there will be no net loss of the kinetic energy during an elastic collision. Even no conversion of the kinetic energy in the other forms takes place when the collision is mainly elastic. **Note:** The things to be on your finger-tips for further information on solving these types of problems are: The units of the given parameters should be taken into consideration while solving the problem.