Question
Question: A mass m moves with a velocity v and collides inelastically with another identical mass. After colli...
A mass m moves with a velocity v and collides inelastically with another identical mass. After collision, the first mass moves with velocity v/3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision.
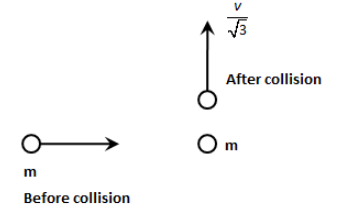
A. 32v
B. 3v
C. v
D. 3v
Solution
We know that in an inelastic collision, the momentum of the system conserves. The second particle is at rest. Use the law of conservation of momentum along the horizontal direction and then along the vertical direction of the motion of the two particles. Solving the two equations simultaneously, you will get the velocity of the second particle.
Formula used:
Momentum, p=mv,
where, m is the mass and v is the velocity.
Complete step by step answer:
The velocity of the second mass after the collision is v′ making an angle θ with the horizontal. We know that in inelastic collision, the momentum of the system conserves.The direction of the second particle is as shown in the figure below.
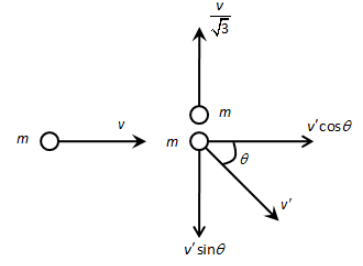
The momentum of the system remains constant along the horizontal direction and along the vertical direction. We have given that the second particle is initially at rest and therefore, the initial momentum of the second particle is zero. Let us express the conservation of linear momentum along the horizontal direction as follows,
pix=pfx
⇒mv+0=0+mv′cosθ
⇒v=v′cosθ …… (1)
The velocity of the first particle after the collision along the horizontal direction is zero.
Let us express the conservation of linear momentum along the vertical direction as follows,
piy=pfy
⇒0+0=m3v−mv′sinθ
⇒3v=v′sinθ …… (2)
Squaring and adding equation (1) and (2), we get,
v2+3v2=v′2cos2θ+v′2sin2θ
⇒34v2=v′2(sin2θ+cos2θ)
⇒34v2=v′2
∴v′=32v
So, the correct answer is option A.
Note: The crucial step in the solution is to determine the velocity of the second particle after the collision since the velocity vector makes some angle with the horizontal. We can use the law of conservation of momentum only along the horizontal direction and vertical direction. Note that, only the momentum is conserved in the inelastic collision, the kinetic energy does not conserve in the inelastic collision.
