Question

A mass m moves with a velocity v and collides in-elastically with another identical mass. After collision the mass moves with velocity $\dfrac{V}{\sqrt{3}}$ in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after the collision.
(A) V
(B) $\sqrt{3}$ v
(C) $\dfrac{2}{\sqrt{3}}$ v
(D) $\dfrac{1}{\sqrt{3}}$ v

Answer 1

An inelastic collision, in contrast to an elastic collision, is a collision in which kinetic energy is not conserved due to the action of internal friction. In collision of macroscopic bodies, some kinetic energy is turned to vibrational energy of the atoms, causing a heating effect, and bodies are deformed. Although inelastic collisions do not conserve kinetic energy, they do obey conservation of momentum.

Complete step by step solution
A mass m moves with a velocity V and collides in- elastically with another identical mass (say B) A moves with velocity $V_{1}^{{}}$ making angle $\theta$ with horizontal after collision and B moves with velocity $\dfrac{V}{\sqrt{3}}$ in the direction perpendicular to the A after the collision.

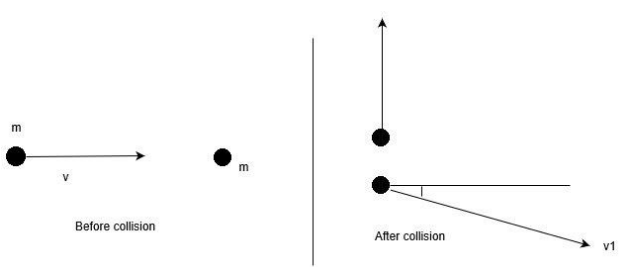
Total momentum before collision and after the collision should be equal that is
${{P}_{i}}={{P}_{f}}$ $\to (A)$
Where, ${{P}_{i}}$ =momentum before collision
${{P}_{f}}$ = momentum after collision
Along X-axis
${{P}_{i}}$ = $mv$
And, ${{P}_{f}}=$ $mv{}_{1}\cos \theta$
According to equation (A)
$\begin{aligned} & mv=mv{}_{1}\cos \theta \\\ & v={{v}_{1}}\cos \theta \\\ & \\\ \end{aligned}$ $\to (1)$
Along Y-axis
${{P}_{i}}=\dfrac{mv}{\sqrt{3}}$
And, ${{P}_{f}}=m{{v}_{1}}\sin \theta$
According to the equation (A)
$\dfrac{mv}{\sqrt{3}}$ $\dfrac{mv}{\sqrt{3}}=m{{v}_{1}}\sin \theta$
$\dfrac{v}{\sqrt{3}}={{v}_{1}}\sin \theta$ $\to (2)$
Now, squaring and adding (1) and (2)
$$ $\begin{aligned} & {{v}^{2}}+\dfrac{{{v}^{2}}}{{{(\sqrt{3})}^{2}}}={{v}_{1}}^{2}{{\cos }^{2}}\theta +{{v}_{1}}^{2}{{\sin }^{2}}\theta \\\ & \\\ \end{aligned}$
${{v}^{2}}+\dfrac{{{v}^{2}}}{3}={{v}_{1}}^{2}\left[ {{\cos }^{2}}\theta +{{\sin }^{2}}\theta \right]$
$\dfrac{4v{}^{2}}{3}={{v}_{1}}^{2}$ , $\left[ \because {{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1 \right]$
${{v}_{1}}=\dfrac{2v}{\sqrt{3}}$
$\therefore$ Option (C) is correct.

Note
A perfectly inelastic collision occurs when the maximum amount of kinetic energy of a system is lost. For example, a high speed car collision is an inelastic collision. Some of the kinetic energy is converted into sound, heat and deformation of the objects.