Question

A mass $M Kg$ is suspended by a weightless string. The horizontal force required to hold the mass at ${60^o}$ with the vertical is
(A) $Mg$
(B) $Mg\sqrt 3$
(C) $Mg\left( {\sqrt 3 + 1} \right)$
(D) $\dfrac{{Mg}}{{\sqrt 3 }}$

Answer 1

Hint We are given with a body suspended by a weightless string and are asked to find the horizontal force required to hold the mass at the given angle. Thus, we will use the work energy theorem to solve the given problem.
Formulae Used:
$W = \Delta T$
Where,$W$ is the work done by the body and$\Delta {\rm T}$ is the change in kinetic energy.

Complete step by step solution

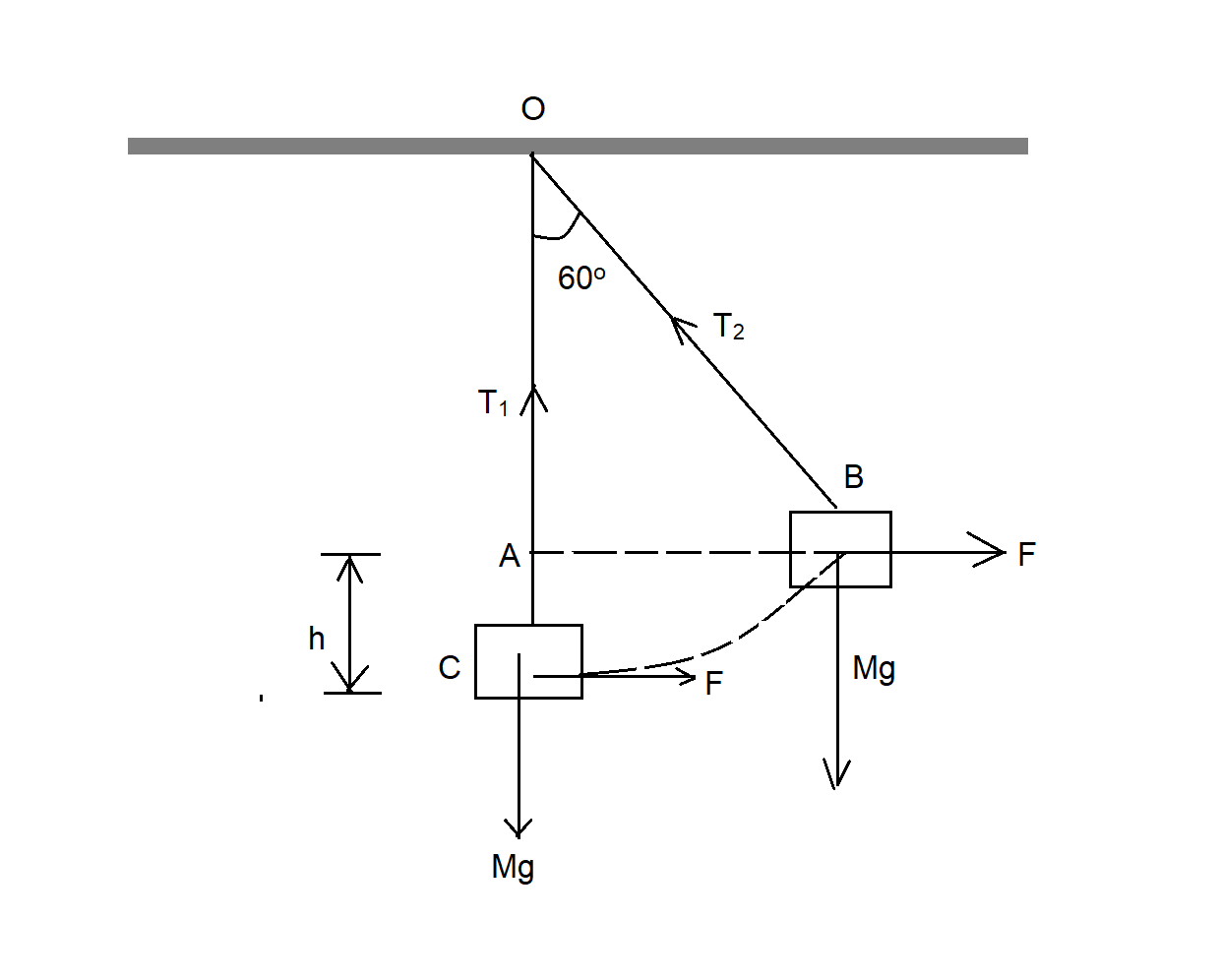
Here,
The total work done is$W = {W_{{T_1}}} + {W_{{T_2}}}$
Where,$W$ is the net work done,${W_{{T_1}}}$ is the work done by the tension${T_1}$ and${W_{{T_2}}}$ is the work done by the tension${T_2}$.
Now,
As the string is the same, then the tension will remain constant.
Thus,
${T_1} = {T_2} = T$
Now,
As per the diagram,
$T = Mg$
Also,
As the horizontal force acting on the body is constant and thus the velocity of the body remains constant and thus, the change in the kinetic energy of the body is$0$.
Thus,
${W_{{T_1}}} + {W_{{T_2}}} = \Delta T$
Then,
${W_{{T_1}}} + {W_{{T_2}}} = 0$
Further, we get
$F \times AC + {F_H} \times AB = 0$
Now,
The force on the body is$T$.
Then, we get
${F_H} = - F\left( {\dfrac{{AC}}{{AB}}} \right)$
Further, we get
${F_H} = \left( { - Mg} \right)\left( {\dfrac{{ - h}}{{AB}}} \right)$
Then, we get
${F_H} = \left( { - Mg} \right)\left( { - \tan {{60}^o}} \right)$
Then, we get
${F_H} = Mg\sqrt 3$

Hence, The correct option is (B).

Note We calculated the answer using the work energy theorem. This is because, for the moving body, we can relate the work done and the energy of the body to a great precision.