Question

A mass m is suspended by a spring and the spring is vibrating with frequency ‘n’. If it is cut into two equal pieces and same mass is suspended by one of the pieces then the new frequency will be
$\text{A}\text{. }n\sqrt{2}$
$\text{B}\text{. }\dfrac{n}{\sqrt{2}}$
$\text{C}\text{. }\dfrac{n}{2}$
$\text{D}\text{. }n$

Answer 1

Use the formula for the frequency of the spring and write an expression for n. Then find the equivalent spring constant when the spring is cut into halves and the two are attached to the mass. With this find the new frequency of the spring.

Formula used:
$f=\dfrac{1}{2\pi }\sqrt{\dfrac{k}{m}}$.

Complete step-by-step answer:
It is given that a mass m is suspended by a spring.
Then the frequency of the oscillations of the spring is given by $f=\dfrac{1}{2\pi }\sqrt{\dfrac{k}{m}}$, where k is the spring constant of the spring.
$\Rightarrow n=\dfrac{1}{2\pi }\sqrt{\dfrac{k}{m}}$ …. (i).
It is given that the spring is cut into two equal halves and the same mass is suspended with the help of one of the springs.
The spring constant of a spring is inversely proportional to its length.
i.e. $k\propto \dfrac{1}{l}$.
Therefore, if the length of the spring is reduced to half then the spring constant of the spring will double.
This means that the new spring constant of the half spring is 2k.
Therefore, the new frequency of the spring will be $n'=\dfrac{1}{2\pi }\sqrt{\dfrac{2k}{m}}$ …. (ii).
Now, divide (ii) by (i).
$\Rightarrow \dfrac{n'}{n}=\dfrac{\dfrac{1}{2\pi }\sqrt{\dfrac{2k}{m}}}{\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m}}}$
$\Rightarrow \dfrac{n'}{n}=\sqrt{2}$
$\Rightarrow n'=n\sqrt{2}$.
This means that the new frequency of the spring is $n\sqrt{2}$.

So, the correct answer is “Option A”.

Note: Suppose both the half springs were attached to the same mass m.

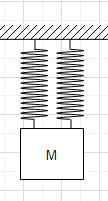
This means that the two springs of equal lengths and spring constant are attached in parallel. Then the equivalent spring constant of this combination is given by ${{k}_{eq}}={{k}_{1}}+{{k}_{2}}$.
In this case, ${{k}_{1}}={{k}_{2}}=2k$.
$\Rightarrow {{k}_{eq}}=2k+2k=4k$.
Therefore, the frequency of oscillation of this combination we be $f=\dfrac{1}{2\pi }\sqrt{\dfrac{{{k}_{eq}}}{m}}$.
$\Rightarrow f=\dfrac{1}{2\pi }\sqrt{\dfrac{4k}{m}}$