Question

A mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
A. $\dfrac{2g}{3}$
B. $\dfrac{g}{2}$
C. $\dfrac{5g}{6}$
D. $g$

Answer 1

It involves the concept of no slipping condition in cases of rotational motion of pulley and translation motion of block. The linear acceleration of block is equal to radius times angular acceleration of pulley, $a=R\alpha$
Also the moment of inertia of the hollow cylinder is $M{{R}^{2}}$.
Also torque equation is to be written for the pulley ,axis passing through the centre of the pulley.
Then by drawing a free body diagram of block, acceleration of block can be found out.

Complete step-by-step answer:

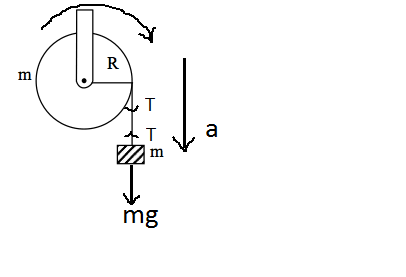
The pulley is moving with angular acceleration and non slipping condition is satisfied with acceleration of the block,
$a=R\alpha ......\left( 1 \right)$
Also the tension force$T$ is actually creating a clockwise torque at the rim of pulley responsible for the rotational motion of the pulley,

The equation for torque is$\tau =TR$
Where R is the perpendicular distance of tension force’s line of action to the rotating axis
also$\tau =I\alpha$where $I$is Moment of inertia of hollow cylinder$\Rightarrow m{{R}^{2}}$
So $TR=I\alpha$
$\Rightarrow TR=m{{R}^{2}}\alpha$
$\Rightarrow T=mR\alpha ......\left( 2 \right)$
Force equation for block,
$mg-T=ma$
from equation (1)
$mg-T=mR\alpha .......\left( 3 \right)$
From $\left( 2 \right)\,and\left( 1 \right)$,
$\Rightarrow mg=ma+ma$
$\therefore a=\dfrac{g}{2}$
So the block will fall down with this acceleration which is option B.

So, the correct answer is “Option B”.

Note: The moment of inertia, otherwise known as the angular mass or rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis.
It is a rotational analogue of mass.
For a point mass the moment of inertia is simply the mass times the square of the perpendicular distance to the axis of rotation. The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems (all taken about the same axis)