Question
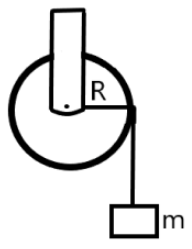
Question: A mass ‘\(m\)’ is supported by a massless string wound around a uniform hollow cylinder of mass \(m\...
A mass ‘m’ is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R . If the string does not slip on the cylinder, with what acceleration will the mass fall on release?
A. 65g
B. g
C. 32g
D. 2g
Solution
Here, we will use the concept of tension to calculate the acceleration of the released mass. Now, as the tension in the string is the same at all the points, therefore, we will equate both the tensions of the string with mass suspended and tension in case of slipping off the string. Hence, we will get the value of acceleration.
Complete step by step answer:
A mass ‘m’ is attached by a massless string that is wounded around a uniform hollow cylinder. Now, according to Newton's second law of motion, the force acting on a body is equal to the product of mass and acceleration.
F=ma
Now, if the tension is produced in the string, than the force is given by
F=mg−T
Now, putting the value of F in the above equation, we get
ma=mg−T
Now, in the case, the string is not slipping on the cylinder. Therefore, the freefall of the suspended mass will be due to acceleration due to gravity.
The linear acceleration a will rise tangentially with the angular acceleration of the string, therefore, the acceleration is given by
a=Rα
Putting this value of acceleration in the above equation, we get
mRα=mg−T
Now, the torque produced by the angular movement of the string is the result of the angular acceleration of the cylinder. Therefore, the torque is given by
τ=I×α
Here, I is the rotational inertia in the cylinder and is given by
I=mR2
Putting this value, the equation of the torque is given by
τ=mR2α
⇒τ=mR2(Ra)
⇒τ=mRa
Which is the rotational torque.
This torque also produces a linear torque and is given by
τ=TR
Now, equating the equations of τ , we get
mRa=TR
⇒ma=T
Now, the tension in the string is given by
T=mg−ma
Therefore, equating both the equations, we get
⇒ma=mg−ma
⇒2ma=mg
⇒2a=g
∴a=2g
Therefore, the mass suspended will fall on release with the acceleration 2g .
Hence, option D is the correct option.
Note: Torque is the measure of the force that can cause an object to rotate about an axis. Force is what causes an object to accelerate in linear kinematics. Similarly, torque is what causes an angular acceleration. Hence, torque can be defined as the rotational equivalent of linear force. The point where the object rotates is called the axis of rotation. In physics, torque is simply the tendency of a force to turn or twist.Now, the torque in linear kinematics is different from the torque in rotational kinematics.
Torque in linear kinematics is τ=r×F .
Torque in rotational kinematics is τ=Iα .
