Question

A mass M is hung with a light inextensible string. Tension in horizontal part of string is:
To solve this question we draw the free body diagram of the given situation. A free body diagram is simply a figure that represents both the direction and magnitude of all the forces acting on that particular system. So for solving similar questions always draw a free body diagram.
$\begin{aligned} & \text{A}\text{. }\sqrt{3}Mg \\\ & \text{B}\text{. }\sqrt{2}Mg \\\ & \text{C}\text{. }\dfrac{Mg}{\sqrt{3}} \\\ & \text{D}\text{. }\dfrac{Mg}{2} \\\ \end{aligned}$

Answer 1

We are given a mass suspended on a string and the figure of the system is given to us. We are asked to find the tension on the horizontal part of the string. To find the tension on the string we can construct the free body diagram of the given situation. From the free body diagram, by equating the forces on the system we will get the solution.

Complete answer:
In the question we have a mass ‘M’ which is hung on a light inextensible string.
To solve the question let us draw the free body diagram of the given situation.

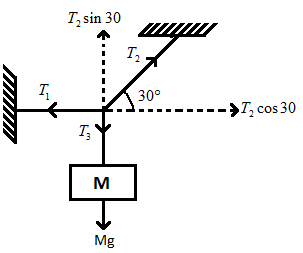
From the figure we can see that ‘${{T}_{1}}$’ is the tension on the horizontal part of the string, ‘${{T}_{2}}$’ is the tension along the string which is at an angle $30{}^\circ$ and ‘${{T}_{3}}$’ is the tension on the string where the mass is suspended.
We can resolve the two components of ‘${{T}_{2}}$’ as ${{T}_{2}}\sin 30$ vertically upwards and ${{T}_{2}}\cos 30$ in the horizontal direction.
The force acting on the system is the weight of the body vertically downwards which is given as $Mg$.
In the question we are asked to find the tension on the horizontal part of the string. From the figure this tension can be written as,
${{T}_{1}}={{T}_{2}}\cos 30$
From the free body diagram we can also see that,
${{T}_{3}}=Mg$ and ${{T}_{2}}\sin 30={{T}_{3}}$
From this two equations, we get
$\Rightarrow {{T}_{2}}\sin 30=Mg$
$\Rightarrow {{T}_{2}}=\dfrac{Mg}{\sin 30}$
Since $\sin 30=\dfrac{1}{2}$, we get
$\Rightarrow {{T}_{2}}=\dfrac{Mg}{\left( \dfrac{1}{2} \right)}=2Mg$
By substituting the value of ‘${{T}_{2}}$’ in the equation for tension on the horizontal part,
${{T}_{1}}={{T}_{2}}\cos 30$, we get
$\Rightarrow {{T}_{1}}=\left( 2Mg \right)\cos 30$
We know that $\cos 30=\dfrac{\sqrt{3}}{2}$, by substituting this we get
$\Rightarrow {{T}_{1}}=2Mg\times \dfrac{\sqrt{3}}{2}$
By solving this equation, we get
$\Rightarrow {{T}_{1}}=\sqrt{3Mg}$
Therefore the tension along the horizontal part of the string is $\sqrt{3Mg}$.

So, the correct answer is “Option A”.

Note:
To solve this question we draw the free body diagram of the given situation. A free body diagram is simply a figure that represents both the direction and magnitude of all the forces acting on that particular system. So for solving similar questions always draw a free body diagram.