Question

A mass $M$ is held in place by an applied force $F$ and a pulley system as shown in figure. The pulley are massless and frictionless.

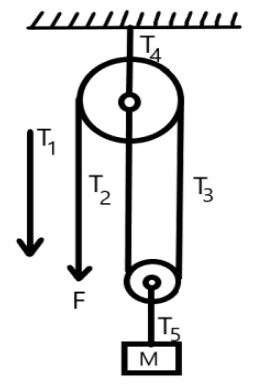
(a) Draw a free body diagram for each pulley
(b) Find tension in each section of rope ${T_1}$ , ${T_2}$ , ${T_3}$ , ${T_4}$
(c) Find the magnitude of $F$

Answer 1

Here, a mass is attached by a string which rolls over the pulley. Here, different tensions will occur in each rope. All, the tensions will act downwards except ${T_4}$ as it is acting in the upward direction. As shown in the figure, the force $F$ will be equal to the tension ${T_1}$.

Complete step by step answer:
Consider a mass which is held by a pulley with a massless string which is shown below

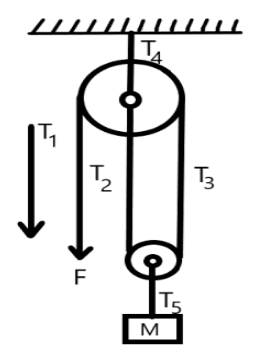
(a) Now, the free diagram of the system shown above is given below


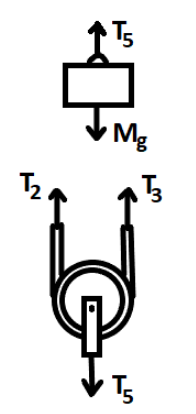
Here all the forces are working in the vertical direction. Now, as the pulleys are massless and frictionless, therefore, the tension in the strings will be the same along the full rope. Also, the downward will be equal to the three tensions that will put the mass. Therefore, $F - {T_1} = 0$

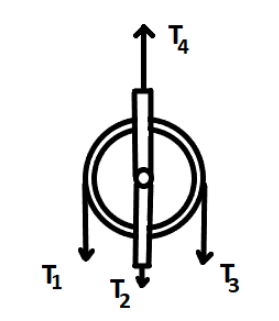
(b) Now, the rope will go through the pulley, therefore, the net force acting downward will be
${T_4} = {T_1} + {T_2} + {T_3}$
Now, the tensions ${T_1}$ , ${T_2}$ and ${T_3}$ are acting downward, therefore, all the tensions will be equal to the weight of the pulley and is given by
${T_1} = {T_2} = {T_3} = \dfrac{{Mg}}{2}$
Therefore the first equation will become
${T_4} = \dfrac{{Mg}}{2} + \dfrac{{Mg}}{2} + \dfrac{{Mg}}{2}$
$\Rightarrow \,{T_4} = \dfrac{{3Mg}}{2}$
Therefore, the tension in each rope is ${T_1} = \dfrac{{Mg}}{2}$ , ${T_2} = \dfrac{{Mg}}{2}$ , ${T_3} = \dfrac{{Mg}}{2}$ and ${T_4} = \dfrac{{3Mg}}{2}$

(c) Now, from the option (a) we can say that the magnitude of force is given by
$F = {T_1}$
$\therefore F = \dfrac{{Mg}}{2}$
Therefore the magnitude is $\dfrac{{Mg}}{2}$ .

Note: Here, we have not talked about the tension ${T_5}$ as it is in the same direction as that of the tension ${T_4}$. Also, it will be equal to the mass of the body that is hanged, that is, ${T_5} = Mg$ . Also, the above system is frictionless and is not rotating.