Question

A mass m is attached to a thin wire and whirled in a vertical circle. The wire is most likely to break when:
A. The mass is at the highest point
B. The wire is horizontal
C. The mass is at the lowest point
D. Inclined at an angle of 60$^\circ$ from vertical

Answer 1

First, we need to draw a free body diagram for the mass moving in a vertical plane. Then we need to find an equation for the tension in the string and compare the tension at the highest and the lowest point. The wire will break at the point where the tension is maximum.

Complete step by step answer:


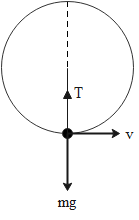
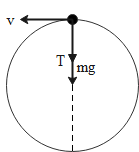
We are given a mass m which is attached to a thin wire and whirled in a vertical circle as shown in the diagram. T represents the tensional force in the wire to stretch the wire, mg is the weight of the mass acting in downward direction while v is the linear velocity of the mass.
Now we know that in order to move a mass in a circular path, we need centripetal force which is provided by the weight of the mass. If we consider the tension in the string acting opposite to the weight of the mass then we can write the following expression when the mass is at lowest point.
$T - mg = \dfrac{{m{v^2}}}{l}$
When the mass is at the highest point, we have
$T + mg = \dfrac{{m{v^2}}}{l}$
Here l is the length of the string which is also the radius of the circle in which the mass revolves.
In order to break the wire, it needs to be stretched with maximum force and this force is the same as the tensional force in the wire. So, the tension needs to be maximum in order for the wire to break. So, at the lowest point, we have
$T = mg + \dfrac{{m{v^2}}}{l}$
At the highest point, we have
$T = \dfrac{{m{v^2}}}{l} - mg$
Therefore, the tension is maximum at the lowest point as compared to the highest point. So, the wire is most likely to break when the mass is at the lowest point.

So, the correct answer is “Option C”.

Note:
It should be noted that the above result holds when the mass is whirled in a vertical plane. In case if the mass is whirled in a horizontal plane then, the tension will remain same at all points of the horizontal plane and the wire has equal probability of breaking at all points of the circular path.