Question

A mass $m$ falls on spring constant $k$ and negligible mass from a height $h$. Assuming it sticks to the pan and executes simple harmonic motion, the maximum height upto which the pan will rise is:
A. $\dfrac{mg}{k}$
B. $\dfrac{mg}{k}\left[ \sqrt{1+\dfrac{2kh}{mg}}-1 \right]$
C. $\dfrac{mg}{k}\left[ \sqrt{1+\dfrac{2kh}{mg}}+1 \right]$
D. $\dfrac{mg}{k}\left[ \sqrt{1+\dfrac{kh}{mg}}-1 \right]$

Answer 1

For this question we will use the formula for potential energy. Potential energy is stored in the spring and after coming in motion potential energy decreases. Making a labeled diagram will help to solve the problem in a systematic way. Concept of simple harmonic motion has also been used. Sign convection should be taken care.

Formula used:
Potential energy $E=mgh$

Complete answer:
Let us consider a mass $m$falling in a spring having spring constant$k$. The mass$m$ is falling from a height $h$. When the mass falls on the spring, the spring compresses and length changes. Let us assume $x$ be the length of the spring after compression, so the total distance from which the spring is falling will be $(h+x)$.

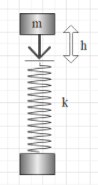
As we know potential energy is stored in the spring and when the system undergoes simple harmonic motion there will be loss of potential energy. This can be given as
$mg(h+x)=\dfrac{1}{2}k{{x}^{2}}$
${{x}^{2}}-\left( \dfrac{2mg}{k} \right)x-\dfrac{2mgh}{k}=0$
Rearranging the terms,

& x=\dfrac{\dfrac{2mg}{k}\pm \sqrt{\left( \dfrac{2mg}{k} \right)2+\dfrac{8mgh}{k}}}{2} \\\ & x=\dfrac{mg}{k}\pm \sqrt{{{\left( \dfrac{mg}{k} \right)}^{2}}+\dfrac{2mgh}{k}} \\\ \end{aligned}$$ $$=\dfrac{mg}{k}\left( 1+\sqrt{\left( 1+\dfrac{2kh}{mg} \right)} \right)$$ In this case we ignore negative sign because if we use negative sign value it also becomes negative and distance is a physical quantity, therefore it can’t be negative. Thus, the maximum height by which the pan rises is $$\dfrac{mg}{k}\left( 1+\sqrt{\left( 1+\dfrac{2kh}{mg} \right)} \right)$$. **Therefore, option C is correct.** **Additional information:** Spring is a system that moves up and down when external force is applied to it. It has numerous applications in our daily life. **Note:** Calculation should be done carefully. At the last step we should be careful of not taking negative signs into consideration because if we take that then distance will be negative and the whole solution will be incorrect. Properties of simple harmonic motion should be read carefully.