Question

A mass is suspended separately by two different springs in successive order then time periods are ${t_1}$ and ${t_2}$ respectively. If it is connected by both springs as shown in the figure then time period is ${t_0}$, the correct relation is

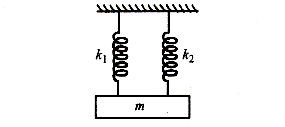
$(A){T_0}^2 = {T_1}^2 + {T_2}^2$
$(B){T_0}^{ - 2} = {T_1}^{ - 2} + {T_2}^{ - 2}$
$(C){T_0}^{ - 1} = {T_1}^{ - 1} + {T_2}^{ - 1}$
$(D){T_0} = {T_1} + {T_2}$

Answer 1

In successive order, a mass is suspended separately by the two different springs. If the same mass is suspended by connecting the two springs in parallel then the time period of oscillations. Calculate the effective force constant of parallel spring then by putting the value of the time period system and we get the new time period spring.

Complete step by step solution:
The figure $1$ shows the time period of a spring-mass system.

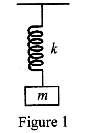
Given by $T = 2\pi \sqrt {\dfrac{m}{k}}$
Where $k$ is the Spring Constant
$\Rightarrow {T_1} = 2\pi \sqrt {\dfrac{m}{{{k_1}}}} .............\left( 1 \right)$
$\Rightarrow {T_2} = 2\pi \sqrt {\dfrac{m}{{{k_2}}}} ................\left( 2 \right)$
Where,
A mass $m$ is suspended separately by two springs of spring constant ${k_1}$ and ${k_2}$ in successive order.${T_1}$ and ${T_2}$are the periods of oscillations in the two cases.

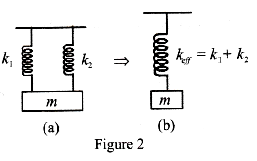
Now, when they are connected in parallel as shown in figure $2$ (a), the system can be replaced by a single spring of spring constant${K_{eff}} = {k_1} + {k_2}$.
Since, $[mg = {k_1}x + {k_2}x = {k_{eff}}x]$
$\therefore {T_0} = 2\pi \sqrt {\dfrac{m}{{{k_{eff}}}}} = 2\pi \sqrt {\dfrac{m}{{\left( {{k_1} + {k_2}} \right)}}} .........\left( 3 \right)$
From$\left[ 1 \right]$, $\dfrac{1}{{{T_1}^2}} = \dfrac{1}{{4{\pi ^2}}} \times \dfrac{{{k_1}}}{m}..........\left( 4 \right)$
From$\left[ 2 \right]$, $\dfrac{1}{{{T_2}^2}} = \dfrac{1}{{4{\pi ^2}}} \times \dfrac{{{k_2}}}{m}..........\left( 5 \right)$
From$\left[ 3 \right]$, $\dfrac{1}{{{T_0}^2}} = \dfrac{1}{{4{\pi ^2}}} \times \dfrac{{{k_1} + {k_2}}}{m}.............\left( 6 \right)$
\left[ 4 \right] + \left[ 5 \right]$$$$ \Rightarrow \dfrac{1}{{{T_1}^2}} + \dfrac{1}{{{T_2}^2}} = \dfrac{1}{{4{\pi ^2}m}}\left( {{k_1} + {k_2}} \right) = \dfrac{1}{{{T_0}^2}}
$\therefore {T_0}^{ - 2} = {T_1}^{ - 2} + {T_2}^{ - 2}$
Hence, the correct answer is the correct relation is option B.

Note: The square root of the mass is proportional to inversely proportional to the period of a spring-mass system and the square root of the spring constant.
The mass will increase as the period increases. More mass-with the same spring-will mean a larger period. A stronger spring-with a larger value of $k$-will move the same mass more quickly for a smaller period. As the spring constant $k$ increases, the period decreases.