Question

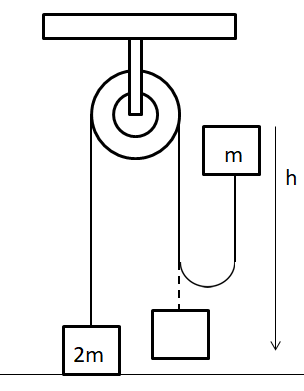
A mass 2m rests on a horizontal table. It is attached to a light inextensible string which passes over a smooth pulley and carries a mass m at the other end. If the mass m is raised vertically to a height h and is then dropped, what is the speed with which the mass 2m begins to rise?

Answer 1

One must know the impulse momentum theorem. According to the impulse momentum theorem, The Impulse (J) of a body is given by; $J={{p}_{final}}-{{p}_{initial}}$, where p is the momentum of the body. The velocity of the body falling from height h is; $v=\sqrt{2gh}$.

Step by step solution:
Let’s first start by understanding the system. The system is initially such that the body of mass (2m) is at rest. The body of mass (m) is initially at rest at a height (h) above the ground. The two bodies are connected to each other through a massless inextensible string over a pulley.
Now, let’s consider the instant, the body of mass (m) falls down from the height (h). Since, the mass (2m) is already at the ground stationary, hence no tension is applied on the string, on the part of the string attached to the body of mass (2m) and neither on the part of the string attached to the body of mass (m). Hence, the velocity of the mass (2m) in this instant is zero. Similarly, the final velocity of the body of mass (m) can be found using the motion law given by: ${{v}^{2}}-{{u}^{2}}=2as\Rightarrow {{v}^{2}}-{{(0)}^{2}}=2gh\Rightarrow v=\sqrt{2gh}$. Hence, the momentum of the particle is; $p=-m\sqrt{2gh}$.
Now let’s consider the instant after the jerk given to the system due to the body of mass (m) dropping. A detailed diagram for this case is given below.

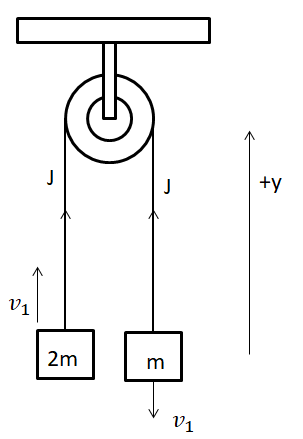
The value of the velocity with which the body of mass (2m) will move upwards can be found using the Impulse momentum theorem, which states that the impulse on a body is equal to the difference of the final and initial momentum of the body. That is; $J={{p}_{final}}-{{p}_{initial}}$.
Hence, applying the Impulse momentum theorem to the body of mass (2m), we see; $J=2m{{v}_{1}}-0\Rightarrow J=2m{{v}_{1}}\to (1)$, since the initial momentum of the body was zero.
Similarly, applying the Impulse momentum theorem to the body of mass (m), we see; $J=-m{{v}_{1}}-\left( -m\sqrt{2gh} \right)\Rightarrow J=m\sqrt{2gh}-m{{v}_{1}}\to (2)$, since the initial momentum of the body was zero.
Using the equations (1) and (2) we get: $2m{{v}_{1}}=m\sqrt{2gh}-m{{v}_{1}}\Rightarrow 3m{{v}_{1}}=m\sqrt{2gh}\Rightarrow {{v}_{1}}=\dfrac{\sqrt{2gh}}{3}$. Hence, the speed with which the body of mass (2m) begins to rise is: ${{v}_{1}}=\dfrac{\sqrt{2gh}}{3}$.

Note:
It’s important to remember that the value of the initial and the final momentum of the body of mass (m) after the jerk are both negative since, both the velocities act in the downward direction. In the current question as per axis convention, we have considered all the values moving upward to be positive and all the values moving downward to be negative.
Hence, the value of the momenta of the body of mass (m) is negative. If the axis convention were reversed we would still arrive at the same solution.