Question

A mark is made on the bottom of a vessel, over this mark a glass slab of thickness $3.5cm$ and refractive index $7/4$ is placed. Now water (refractive index $4/3$) is poured into the vessel so that the surface of water is $8cm$ above the upper surface of the slab. Looking down normally through the water, the apparent depth of the mark below the surface of water will be:

Answer 1

Apparent depth in a medium is the depth of a body in a denser medium as seen from a rarer medium. The apparent depth in a given medium is less than its real depth.
The apparent depth in a given medium of a body is the ratio of its real depth and refractive index of the medium.

Complete step by step answer:
Let’s draw the figure which depicts the question.

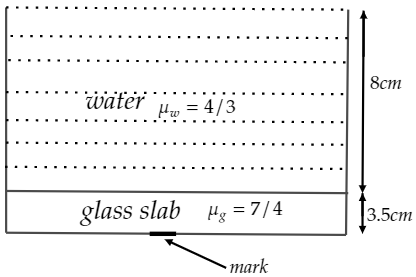
It is given that the thickness of glass slab is $t = 3.5cm$,
The refractive index of the glass slab is ${\mu _g} = \dfrac{7}{4}$,
The real depth of water is $d = 8cm$,
And the refractive index of water is ${\mu _w} = \dfrac{4}{3}$.
We know that the apparent depth $\left( {{d_{apparent}}} \right)$ in a given medium is the ratio of real depth $\left( {{d_{real}}} \right)$ and refractive index $\left( \mu \right)$ of the medium.
${d_{apparent}} = \dfrac{{{d_{real}}}}{\mu }$
Since the observer looking down normally through two different types of medium, the apparent depth of the mark on the bottom of the vessel will be
${d_{apparent}} = \dfrac{{{d_{glass}}}}{{{\mu _{glass}}}} + \dfrac{{{d_{water}}}}{{{\mu _{water}}}}$
Substitute all the required values in the above formula.
${d_{apparent}} = \dfrac{{3.5}}{{\dfrac{7}{4}}} + \dfrac{8}{{\dfrac{4}{3}}}$
Further simplifying
${d_{apparent}} = 2 + 6$
$\Rightarrow {d_{apparent}} = 8cm$
Hence, the apparent depth of the mark on the bottom of the given vessel will be $8cm$.

Note: From Snell's law the formula for apparent depth in a given medium can be derived easily.
The Snell’s law states that the ratio of the sine angle of incidence to the sine angle of refraction is constant for the two media.
i.e., if a ray of light goes from medium 1 to medium 2, then $\dfrac{{\sin i}}{{\sin r}} = {}^1{\mu _2}$
Where, $i$ is the angle of incidence, $r$ is the angle of refraction.
${}^1{\mu _2} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$
${\mu _1}$ and ${\mu _2}$ are the refractive index of medium 1 and 2 respectively.