Question
Question: A marginal ray is falling on a concave spherical mirror as shown in the figure below. The ratio of l...
A marginal ray is falling on a concave spherical mirror as shown in the figure below. The ratio of longitudinal (x) and transverse (y) spherical aberration is:
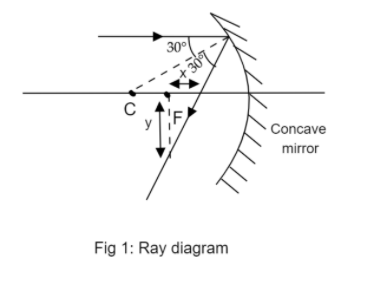
(a) 3
(b) 31
(c) 32
(d) can’t be determined
Solution
This question doesn’t involve much physics, it can be solved by applying concepts of geometry and trigonometry. The reflected ray acts as a transverse for the parallel lines (incident ray and optical axis).
Formula used:
1. Ratio of perpendicular and base for a right angled triangle: tanθ=bp ……(1)
Where,
θ is the angle from the base
p is the perpendicular
b is the base
Complete step by step answer:
The given ray diagram is:
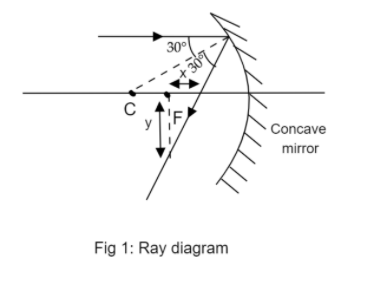
To find: The ratio of longitudinal (x) and transverse (y) spherical aberration.
Step 1 of 2:
The marginal ray given in the diagram is parallel to the optical axis. The reflected ray cuts a pair of these parallel lines. Therefore, the angle it makes with the marginal ray will be equal to the angle it makes with the optical axis.
The angle made by reflected ray with the marginal ray is the summation:
θ=30∘+30∘
θ=60∘
Step 2 of 2:
Consider the triangle ΔFGHin fig 2 with the right angle at F. Now, ∠FGHis the angle θ we just found. Use eq (1) to find the ratio xy:
xy=tanθ
xy=tan60∘
xy=3
Inverting this to find the required ratio yx:
yx=31
The ratio of longitudinal (x) and transverse (y) spherical aberration is 31. Hence option (b) is correct.
Note:
Here, one should take care that just outside the metal surface, for point P metal plate appears infinitely big, therefore, we can use field produced due to infinite metal plate carrying charge approximation.
