Question

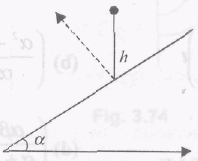
A marble starts falling from rest on a smooth inclined plane of inclination α. After covering distance h the ball rebounds off the plane. The distance from the impact point where the ball rebounds for the second time is

• A. 8h cosα
• B. 8h sin α
• C. 2h tan α
• D. 4h sin α

Answer 1

Answer: (B)

8h sin α

Answer 2

Velocity before strike u = √2gh

Component of acceleration along the inclined plane = g sin α and the perpendicular component = g cos α

Using S = ut + 1/2 at²

For vertical direction we get,

0 = v cos αt – 1/2 g cosαt² and

For horizontal direction

x = u sinαt + 1/2 g sin αt²

= u sin α $\frac{2u}{g} + \frac{1}{2}g\sin\alpha\left( \frac{2u}{g} \right)^{2}\left( Qt = \frac{2u}{g} \right)$

= $\frac{2u^{2}\sin\alpha}{g} + \frac{2u^{2}\sin\alpha}{g} = \frac{4u^{2}\sin\alpha}{g}$

= 4 × $\frac{2gh \times \sin\alpha}{g}$ = 8h sin α