Question

A manufacturing company makes two types of teaching aids A and B of mathematics for class XII. Each type of A requires 9 labour hours of fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours per week are 180 and 30 respectively. The company makes a profit of 80 on each piece of type A and 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week?

Answer 1

First of all assume that pieces of type A and type B manufactured per week are x and y respectively.
The condition for maximum profit per week is the addition of the result of the multiplication of profit of 80 by x and profit of 120 by y. Write the condition for maximum labour hours per week for fabricating finishing individually in which you have to write the condition for fabricating hours that labour put for type A and B pieces. Similarly, finishing hours that labour put in for type A and type B pieces. Using this condition, maximize the profit per week.

Complete step-by-step answer:
Let us assume that x number of pieces of type A are manufactured per week and also let us assume that y number of pieces of type B are manufactured per week.
It is given that the company makes a profit of 80 on each piece of type A and 120 on each piece of type B so the total profit for pieces of type A and type B is calculated by multiplying the number of pieces of each type by their corresponding profit given.
Profit of type A piece is calculated by multiplying x to 80 which we have shown below.
$80\left( x \right)$
Profit of type B piece is calculated by multiplying y to 120 which we have shown below:
$120\left( y \right)$
Total profit for type A and type B piece is equal to:
$80x+120y$
Let us represent the total profit by “Z” that we have to maximize.
$Z=80x+120y$……….Eq. (1)
The number of labour hours per week for each piece of type A for fabricating is 9 so for x number of pieces the total labour hours per week for type A for fabrication is equal to:
$9\left( x \right)$…….Eq. (2)
The number of labour hours per week for each piece of type B for fabricating is 12 so for y number of pieces the total labour hours per week for type B for fabrication is equal to:
$12y$……….Eq. (3)
Total fabricating labour hours per week for type A and type B pieces is equal to sum of equations (1 & 2).
$9x+12y$
It is given that the maximum fabricating labour hours per week are 180 so maximizing $9x+12y$ we get,
$9x+12y\le 180$
Dividing the above by 3 we get,
$3x+4y\le 60$……….. Eq. (4)
Finishing labour hours per week for each piece of type A is given as 1 hour and finishing labour hours per week for each piece of type B is given as 3 hours.
Similarly, we can write total finishing labour hours per week for type A and type B as:
$x+3y$
Now, the maximum fabricating labour hours per week is given as 30 so maximizing the above relation we get,
$x+3y\le 30$………. Eq. (5)
As the number of pieces of type A and type B are x and y and number of pieces are the counting numbers so the number of pieces must be non negative.
$x\ge ,y\ge 0$…………….. Eq. (6)
In the below figure, we have plotted eq. (4, 5 & 6) on the graph in which you can see that the intersection of these inequalities are the points A(12, 6), B(20, 0) and C(0, 10).

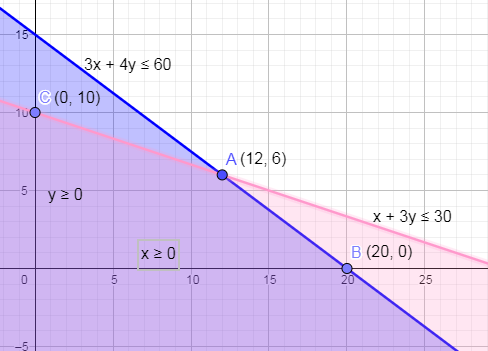
Substituting the points A, B and C in eq. (1) we get,
Substituting point A (12, 6) in eq. (1) we get,
$\begin{aligned} & Z\left( x,y \right)=80x+120y \\\ & \Rightarrow Z\left( 12,6 \right)=80\left( 12 \right)+120\left( 6 \right) \\\ & \Rightarrow Z\left( 12,6 \right)=960+720 \\\ & \Rightarrow Z\left( 12,6 \right)=1680 \\\ \end{aligned}$
Substituting point B (20, 0) in eq. (1) we get,
$\begin{aligned} & Z\left( x,y \right)=80x+120y \\\ & \Rightarrow Z\left( 20,0 \right)=80\left( 20 \right)+120\left( 0 \right) \\\ & \Rightarrow Z\left( 20,0 \right)=1600 \\\ \end{aligned}$
Substituting point C (0, 10) in eq. (1) we get,
$\begin{aligned} & Z\left( x,y \right)=80x+120y \\\ & \Rightarrow Z\left( 0,10 \right)=80\left( 0 \right)+120\left( 10 \right) \\\ & \Rightarrow Z\left( 0,10 \right)=1200 \\\ \end{aligned}$
As you can see that when substituting the point A we have got the maximum value of Z i.e. 1680.
Hence, the maximum profit is Rs 1680.

Note: The problem that you could face in the above problem is in writing the inequality in maximum condition. For instance, in the above solution we have given the maximum fabricating and finishing hours so you might have thought that in the maximum condition which inequality should be there either $\le$ or $\ge$. The solution to this problem is that we have given the maximum fabricating and finishing hours which means that these numbers of hours (which is the maximum value) or less than that is possible only so $\le$ this inequality will come for maximum.