Question

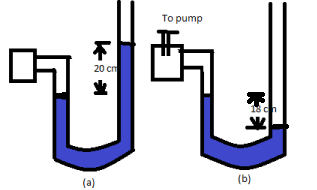
A manometer reads the pressure of a gas in an enclosure as shown in fig (a). When a pump removes some of the gas, the manometer reads as in fig (b). The liquid used in the manometers is mercury and the atmospheric pressure is $76\,cm$ of mercury.
a. Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), in units of $cm$ of mercury.
b. How would the levels change in case (b) if $13.6\,cm$ of water (immiscible with mercury) are poured into the right limb of the manometer? (Ignore the small change in the volume of the gas.

Answer 1

Here for case (1) in figure (a) and figure (b) we have to calculate the absolute pressure using the formula of absolute pressure.
For case (2) we have to first calculate the pressure for the right and left limb and then equate them to find the height.

Complete step by step solution:
Given,
Atmospheric pressure ${P_ \circ } = 76\,cm\,\,{\text{of}}\,{\text{Hg}}$
Case (1)
For figure (a)
Gauge pressure is given by the gap between the mercury levels in the two limbs.
So, Gauge pressure $= 20\,cm\,\,{\text{of}}\,{\text{Hg}}$
We know that,
Absolute pressure = atmospheric pressure + gauge pressure
$= 76\,cm + 20\,cm = 96\,cm\,\,{\text{of}}\,{\text{Hg}}$

For figure (b)
Difference between mercury amounts in the two limbs $= - 18\,cm$
So, gauge pressure $= - 18\,cm\,\,{\text{of}}\,{\text{Hg}}$

Absolute pressure = atmospheric pressure + gauge pressure
$= 76\,cm - 18\,cm = 58\,cm$

Case (2)
Given, $13.6\,cm$ of water (immiscible with mercury) is poured into the right limb of the manometer.
So, relative density of mercury $= 13.6\,cm$

Therefore, $1\,cm$ of mercury is equal to a column of $13.6\,cm$ of water.
Now, let the difference between the mercury levels in the two limbs be $h$
So, the right limb pressure is given by-
Pressure = atmospheric pressure + $1\,cm\,\,{\text{of}}\,{\text{Hg}}$
$= 76 + 1 = 77\,cm\,\,{\text{of}}\,{\text{Hg}}$ ...... (i)

In the left limb, the mercury column will rise.
Hence, pressure in the left limb-
Pressure= atmospheric pressure + $1\,cm\,\,{\text{of}}\,{\text{Hg}}$
$= 58 + h$ ...... (ii)

From equations (i) and (ii), we get-
$77 = 58 + h \\\ h = 19\,cm \\\$
Hence, the levels change in case (b) if $13.6\,cm$ of water (immiscible with mercury) are poured into the right limb of the manometer by $19\,cm$.

Note:
Here we have to be careful for the gauge pressure in case of figure (b), as the gauge pressure here is of negative value since the level of mercury is less in the right limb than in the left limb.