Question
Question: A man wants to reach point B on the opposite bank of the river flowing at a speed as shown in the fi...
A man wants to reach point B on the opposite bank of the river flowing at a speed as shown in the figure. What minimum speed relative to water should the man have so that he can reach point B?
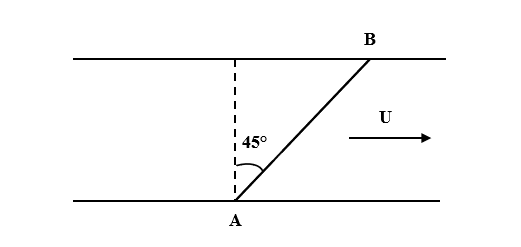
Solution
To solve this problem, consider V as the velocity of the man and VB as the resultant of U and V. Then, find the components of VB in X and Y axes. Then, find the relation between 45° and components of VB along X-axis and Y-axis. Substitute the values of the components and solve it to get an equation for V in terms of U. Substitute the condition for V to be minimum and find V. This will give the minimum velocity of man to reach point B.
Complete answer:
Let V be the speed of the man in still water.
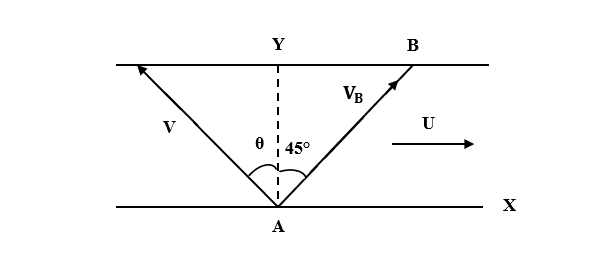
Resultant of U and V should be along AB.
Let VB be the absolute velocity of man.
Component of VB along X-axis can be given by,
VX=U–Vsinθ …(1)
Component of VB along Y-axis can be given by,
VY=Vcosθ …(2)
In △YAB,
tanθ=AdjacentsideOppositeside
Substituting values in above equation we get,
tan45°=VXVY
⇒1=VXVY …(3)
Substituting equation. (1) and equation. (2) in equation. (3) we get,
1=U–VsinθVcosθ
⇒U–Vsinθ = Vcosθ
⇒U = Vsinθ+Vcosθ
⇒U= V(sinθ+cos0θ)
⇒V= sinθ+cosθU …(4)
We know, usinθ+vcosθ= u2+v2
⇒sinθ+cosθ = 2
⇒V = 2sinθ+45°U …(5)
V will be minimum at,
θ+45°= 90°
⇒θ = 45°
Substituting this value in the equation. (5) we get,
Vmin = 2sin45°+45°U
⇒Vmin = 2sin90°U
⇒Vmin= 2U
Hence, the man should have a relative speed of 2U to reach point B.
Note:
If the man has to cross the river and reach the exact opposite bank of the river then the velocity of swimming of man should always be greater than the velocity of the flow of the river. If the velocity of the flow of the river is larger than the velocity of the man then the man can never reach the point exactly opposite to the bank. In this question, the man does not have to reach the exact opposite bank of the river. Hence, the velocity of swimming of the man is less than the velocity of the flow of the river.
