Question

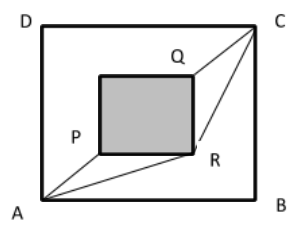
A man wants to reach from A to the opposite corner of the square C (Fig). The sides of the square are 100 m. a central square of 50 m is filled with sand. Outside this sand, he can walk at speed 1 m/s. in the central square, he can walk only at a speed of v m/s (v<1). What is the smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand?

A) $0.18{\text{ m}}{{\text{s}}^{ - 1}}$
B) $0.87{\text{ m}}{{\text{s}}^{ - 1}}$
C) $0.81{\text{ m}}{{\text{s}}^{ - 1}}$
D) $0.95{\text{ m}}{{\text{s}}^{ - 1}}$

Answer 1

On this question we have to find the smallest value of v for which the man can reach faster via a straight path through the sand than any path in the square outside the sand. To find this we will use the formula of distance between two points and the formula of time.

Complete step by step solution:
Given:
The side of the square = 100 m
The side of central square = 50 m
The speed of the man outside the central square = 1m/s
The speed of the man in the central square = v m/s
The distance between points A and C, $AC = \sqrt {{{(100)}^2} + {{(100)}^2}}$
$\Rightarrow AC = 100\sqrt 2 {\text{ m}}$
The distance between points P and Q,$PQ = \sqrt {{{(50)}^2} + {{(50)}^2}}$
$\Rightarrow PQ = 50\sqrt 2 {\text{ m}}$
$\Rightarrow AP = \dfrac{{AC - PQ}}{2}$
$\Rightarrow AP = \dfrac{{100\sqrt 2 - 50\sqrt 2 }}{2}$
$\Rightarrow AP = 25\sqrt 2 {\text{ m}}$
By using Pythagoras theorem, we can find the values of AR and RC.
$\Rightarrow AR = \sqrt {A{P^2} + P{R^2}}$
$\Rightarrow AR = \sqrt {{{\left( {25\sqrt 2 } \right)}^2} + {{\left( {50} \right)}^2}}$
$\Rightarrow AR = 25\sqrt {10} {\text{ m}}$
$\Rightarrow RC = \sqrt {Q{R^2} + Q{R^2}}$
$\Rightarrow RC = \sqrt {{{\left( {25\sqrt 2 } \right)}^2} + {{\left( {50} \right)}^2}}$
$\Rightarrow RC = 25\sqrt {10} {\text{ m}}$
If we consider the path APQC through the sand and the time to travel from A to C is $\Rightarrow {T_{sand}}$ then time to go from A to C will be
$\Rightarrow {T_{sand}} = \dfrac{{AP + QC}}{1} + \dfrac{{PQ}}{v}$
$\Rightarrow {T_{sand}} = \dfrac{{25\sqrt 2 + 25\sqrt 2 }}{1} + \dfrac{{50\sqrt 2 }}{v}$
$\Rightarrow {T_{sand}} = 50\sqrt 2 \left[ {1 + \dfrac{1}{v}} \right]{\text{ s}}$
Outside the central square the shortest path will be an arc ARC. If the time taken to go through the outside path is${T_{outside}}$. Then the time taken from A to C via this path will be
$\Rightarrow {T_{outside}} = \dfrac{{AR + RC}}{1}$
$\Rightarrow {T_{outside}} = \dfrac{{25\sqrt {10} + 25\sqrt {10} }}{1}$
$\Rightarrow {T_{outside}} = 50\sqrt {10} {\text{ s}}$
Since, it is given that the time taken by sand path is less than outside path
$\Rightarrow {T_{sand}} < {T_{outside}}$
$\Rightarrow 50\sqrt 2 \left[ {1 + \dfrac{1}{v}} \right] < 50\sqrt {10}$
$\Rightarrow \left[ {1 + \dfrac{1}{v}} \right] < \sqrt 5$
$\Rightarrow \dfrac{1}{v} < \sqrt 5 - 1$
$\Rightarrow \dfrac{1}{v} < 2.236 - 1$
$\Rightarrow \dfrac{1}{v} < 1.236$
$\Rightarrow \dfrac{1}{{1.236}} < v$
$\Rightarrow v > 0.809$
$\Rightarrow v > 0.81{\text{ m/}}{{\text{s}}^{ - 1}}$
Hence, the smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand is $v > 0.81{\text{ m/}}{{\text{s}}^{ - 1}}$.

Hence, option (C) is correct.

Note: In such questions we have to be careful about the paths taken and about the calculation also. The knowledge of formulas as well as of theories of distance, time and velocity is must. In this question we had to find the smallest value of v. For this we have done relevant steps and one more thing that we should be careful about is the greater than or smaller than symbol.