Question

A man walks 8 m towards East and then 6 m towards North. His magnitude of displacement is equal to:
${\text{A}}{\text{. }}10m \\\ {\text{B}}{\text{. }}14m \\\ {\text{C}}{\text{. }}2m \\\ {\text{D}}{\text{. zero}} \\\$

Answer 1

Here we first start by making the diagram with direction and show all the data on it. And then from that figure we will easily find out the total displacement that the man traveled.

Complete answer:
Here by the figure let the man travel distance AB due east 8m and then travel distance BC due north 6m.
We have to find out the magnitude of the displacement.

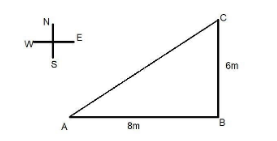
As we know that displacement means the change in position of an object. It is a vector quantity and has a direction and magnitude and in short we can also say that the shortest distance between the starting point and the final point.
So here the shortest distance between point AC is the line joining it.
So we will find it out by using Pythagoras theorem
I.e. $AC = \sqrt {{{\left( {AB} \right)}^2} + {{\left( {BC} \right)}^2}}$ now put the data in the formula we get,
$\Rightarrow AC = \sqrt {{{\left( 8 \right)}^2} + {{\left( 6 \right)}^2}} = \sqrt {64 + 36} = \sqrt {100} = 10m$
Hence the displacement is equal to 10m.
We will also solve such a question by using vector method,
Let the east direction to be $\hat i$ and north direction be$\hat j$.
Thus displacement of the man $\overrightarrow S = 8\hat i + 6\hat j$
And we know that the method to how to take the magnitude of the vector quantity we take mod of it for the magnitude.
So, magnitude of displacement $\left| {\overrightarrow S } \right| = \sqrt {{8^2} + {6^2}} = \sqrt {64 + 36} = 10m$

So, the correct answer is “Option A”.

Note:
Whenever we face such a type of question the key concept for solving the question is to draw the diagram as question says and find the minimum distance but for easy solving always try to solve it by the vector method write the direction in vector form and then find its mod value for the magnitude of the displacement.