Question

A man walks 30 m towards north, then 20 m towards east and in the last $30\sqrt 2 \,m$, towards south-west. The displacement from origin is
A. 10 m towards west
B. 10 m towards east
C. $60\sqrt 2 \,m$ towards northwest
D. $60\sqrt 2 \,m$ towards east north

Answer 1

Use the formula for position vector of a certain point in x-y plane. Calculate the x and y components of south-west displacement of the man. Add the total displacement with respect to its direction.

Formula used:
$\vec S = x\hat i + y\hat j$
Here, x is the x-coordinate and y is the y-coordinate.

Complete step by step answer:
The position vector of point P in x-y plane is given as,
$\vec S = x\hat i + y\hat j$
Here, x is the x-coordinate and y is the y-coordinate.
The displacement of a man is can be drawn as shown in the figure below,

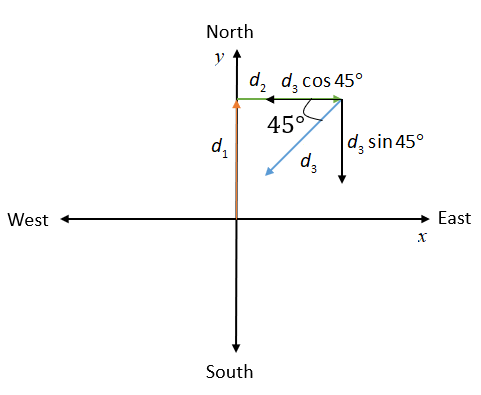
Here, the orange straight-line (${d_1}$) represents the northward displacement, yellow straight-line (${d_2}$) represents eastward displacement and blue straight-line (${d_3}$) represents south-west displacement.
Therefore, the total displacement of a man from origin is,
$\vec S = \left( {{d_2} - {d_3}\cos 45^\circ } \right)\hat i + \left( {{d_1} - {d_3}\sin 45^\circ } \right)\hat j$
Here, ${d_3}\cos 45^\circ$ is the x-component of south-west displacement and ${d_3}\sin 45^\circ$ is the y-component of south-west displacement,
Substitute 30 m for ${d_1}$, 20 m for ${d_2}$ and $30\sqrt 2 \,m$ for ${d_3}$ in the above equation.
$\vec S = \left( {20 - 30\sqrt 2 \cos 45^\circ } \right)\hat i + \left( {30 - 30\sqrt 2 \sin 45^\circ } \right)\hat j$
$\Rightarrow \vec S = \left( {20 - 30} \right)\hat i + 0\hat j$
$\Rightarrow \vec S = - 10\hat i$
The negative sign implies that the displacement is along the negative direction that is towards west. Therefore, the net displacement from the origin is 10 m towards the west.

So, the correct answer is “Option A”.

Note:
Always specify the direction of the displacement vector.
In this question, we have taken the east and north as positive directions and west and south as negative directions.