Question

A man walking with a speed $V$ (constant in magnitude and direction) passes under a lantern hanging at a height $H$ above the ground (consider lantern as a point source). Find the velocity with which the edge of the shadow of the man’s head moves over the ground, if his height is $h$ .
(A) $\dfrac{{Vh}}{{H - h}}$
(B) $\dfrac{{Vh}}{{H + h}}$
(C) $\dfrac{{VH}}{{H - h}}$
(D) $\dfrac{{VH}}{{H + h}}$

Answer 1

For the given condition, construct the diagram. From that identify the similar triangles and construct the relation. Substitute the known parameters and the distance formula in it. Simplifying the obtained relation provides the value of the velocity.
Useful formula:
The formula of the distance is given by
$d = vt$
Where $d$ is the distance, $v$ is the velocity and $t$ is the time taken.

Complete step by step solution:
It is given that the speed of walking by the man is $V$ , height of the lantern is $H$ and height of the man is $h$ .
Let us consider that the shadow of the man moves with the velocity $V'$ .
Let us construct the diagram for the given conditions.

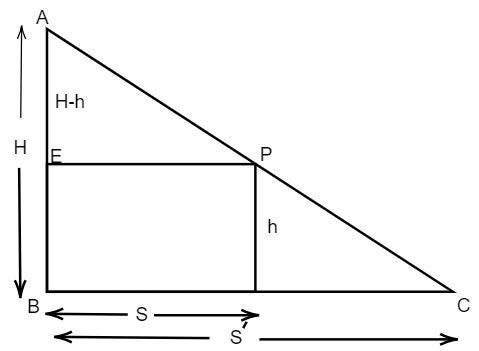
From the above diagram, it is clear that the $\Delta ACB$ is similar to $\Delta ADE$ , so
$\dfrac{{ED}}{{AE}} = \dfrac{{BC}}{{AB}}$
Substituting the known parameters in the above step, we get
$\dfrac{S}{{H - h}} = \dfrac{{S'}}{H}$
Substituting the formula of the distance in the above step, we get
$\dfrac{{Vt}}{{H - h}} = \dfrac{{V't}}{H}$
By cancelling the similar terms in both sides of the equation and simplifying the above step, we get
$V' = \dfrac{{VH}}{{H - h}}$
Hence the velocity at which the shadow edge of the man moves over the ground is $\dfrac{{VH}}{{H - h}}$ .

Thus the option (C) is correct.

Note: The similar triangle theorem is substituted in the above solution. Remember that in this problem, from the constructed diagram, equating the ratio of the base and the height of the triangles. The side $EP$ is taken as $S$ because in the rectangles, the opposite sides are equal.