Solveeit Logo
Login

Question

Question: A man walking with \(3km/h\) feels as if rain is falling at \(60{}^\circ \) with vertical, when he i...

A man walking with 3km/h3km/h feels as if rain is falling at 60∘60{}^\circ with vertical, when he increases his speed to 6km/h he feels that rain is coming at 30∘30{}^\circ with vertical. Find the actual speed of rain.

Explanation

Solution

As a first step, you could find the expression for relative velocity of rain with respect to the walking man. Then, depict the given situation in a neat diagram and then form two equations in the two cases in terms of the vertical component and actual speed of rain. Now solving them will give you the required answer.
Formula used:
Relative velocity,
vrm=vr−vm{{v}_{rm}}={{v}_{r}}-{{v}_{m}}

Complete answer:
In the question, we are given two cases of a man walking in the rain of velocity vr{{v}_{r}} with respect to ground. In the first case, the man is walking at a speed of 3km/h3km/h and he feels as if rain is falling at 60∘60{}^\circ with the vertical. In the second case, the man walking at 6km/h6km/h feels as if the rain is falling at 30∘30{}^\circ with vertical. We are supposed to find the actual speed of rain.
For the first case,

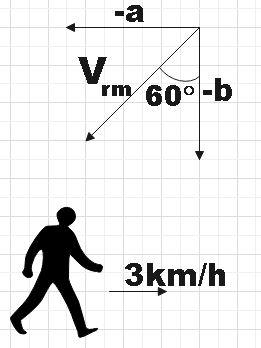
We know that relative velocity of rain with respect to man is given by,
vrm=vr−vm{{v}_{rm}}={{v}_{r}}-{{v}_{m}} ………………………………………………. (1)
Where, vr{{v}_{r}} is the velocity of rain and vm{{v}_{m}} is the velocity of man.
When,vm=3km/h{{v}_{m}}=3km/h, equation (1) would become,
vrm=vr−3{{v}_{rm}}={{v}_{r}}-3……………………………………………………… (2)
But from the figure, we see that,
cos⁡60∘=−bvrm\cos 60{}^\circ =\dfrac{-b}{{{v}_{rm}}}
∴vrm=−2b\therefore {{v}_{rm}}=-2b
So (2) now becomes,
−2b=vr−3-2b={{v}_{r}}-3…………………………………………………… (3)
Now for the second case,

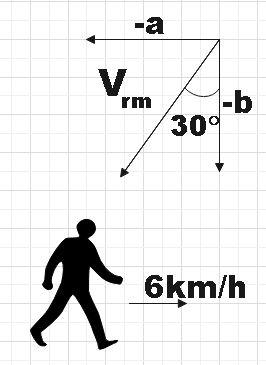
The relative velocity given by (1) becomes,
vrm=vr−6{{v}_{rm}}={{v}_{r}}-6…………………………………………………….. (4)
But from the figure, we see that,
cos⁡30∘=−bvrm\cos 30{}^\circ =\dfrac{-b}{{{v}_{rm}}}
∴vrm=−2b3\therefore {{v}_{rm}}=\dfrac{-2b}{\sqrt{3}}
So (2) now becomes,
−2b=3vr−63-2b=\sqrt{3}{{v}_{r}}-6\sqrt{3}…………………………………………………… (5)
Subtract (3) from (5) to get,
(3−1)vr−63+3=0\left( \sqrt{3}-1 \right){{v}_{r}}-6\sqrt{3}+3=0
⇒(3−1)vr=63−3\Rightarrow \left( \sqrt{3}-1 \right){{v}_{r}}=6\sqrt{3}-3
⇒vr=63−33−1=7.3920.732\Rightarrow {{v}_{r}}=\dfrac{6\sqrt{3}-3}{\sqrt{3}-1}=\dfrac{7.392}{0.732}
∴vr≈10km/h\therefore {{v}_{r}}\approx 10km/h
Therefore, we found that the actual velocity of the rain is 10km/h.

Note:
In both the cases we could clearly see that the horizontal component of relative velocity of the rain with respect to the man is always negative of the velocity of the man. So, for the first case,
a=−3km/ha=-3km/h
And for the second case,
a=−6km/ha=-6km/h
Also, you should understand that by increasing the pace by the walking man only changes the relative velocity of rain and thus in both cases the velocity of rain is the same.