Question

A man uses a concave mirror for shaving. He keeps his face at a distance of twenty centimeters from the mirror and gets an image that is $1.5$ times enlarged. Find the focal length of the mirror.

Answer 1

We can solve this problem with the formula of the focal length of the concave mirror. A concave mirror has concavity facing forwards where the light rays incidents. It is also known as a converging mirror. Concave mirror forms images that are real or virtual, inverted or erect and magnified, reduced, or be similar in size of the object depending upon the positions. Magnification is equal to the negative of the ratio of the distance of the image from the mirror to the distance of the object from the mirror. Magnification $m = \dfrac{{AB}}{{A'B'}}$ and $m = - \dfrac{V}{u}$, where $AB$ is the height of image and $A'B'$ is the height of object.

Formula used:
$\dfrac{1}{V} + \dfrac{1}{u} = \dfrac{1}{F}$ where if $F$ focal length of mirror, $V$ is the image distance and $u$ is the object distance.

Complete step-by-step solution:
If an object is placed in front of a concave mirror then an image is formed at the front of the mirror. This image is inverted, real, and larger than the object. The figure is shown below:

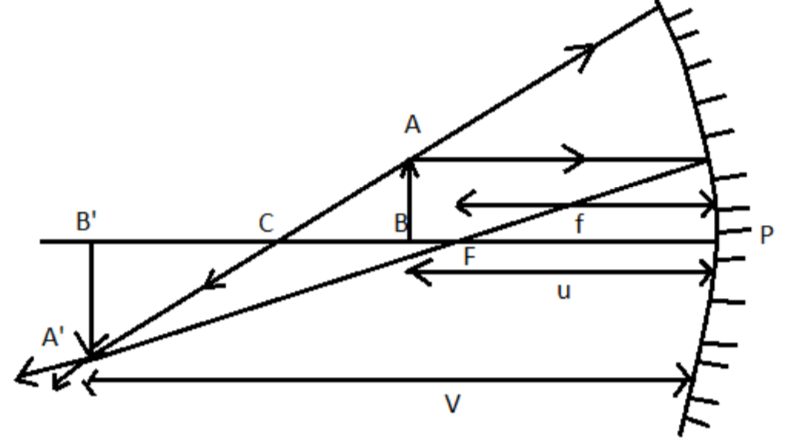
Given that,
Distance of object i.e. $u = - 20cm$
Magnification $= 1.5$
Consider the distance of image $= V$
As we know that magnification is equal to the negative of the ratio of the distance of the image from the mirror to the distance of the object from the mirror.
1.5 = \dfrac{{ - V}}{{ - 20}} \\\ \Rightarrow V = 30cm \\\
Now using the mirror formula:
$\Rightarrow \dfrac{1}{V} + \dfrac{1}{u} = \dfrac{1}{F} = \dfrac{1}{{30}} - \dfrac{1}{{20}} = \dfrac{1}{F} \\\ \Rightarrow \dfrac{{2 - 3}}{{60}} = \dfrac{1}{F} \\\ \Rightarrow F = - 60cm$

Note: In this question, object distance and magnification are given hence we calculated the distance of image as thirty centimeters after that we applied the values in the mirror formula i.e. $\dfrac{1}{V} + \dfrac{1}{u} = \dfrac{1}{F}$ and calculated the focal length of the concave mirror as $60cm$. The image is real, enlarged, and inverted.