Question

A man travels a distance of $1.5$ m towards east, then 2 m towards south and finally $4.5$ m towards east. What is the total distance travelled and displacement?

Answer 1

Hint The total distance is simply the sum of all the little distances travelled. The displacement can be said to be the length of the line drawn from the start of the journey to the end of the journey.
Formula used: In this solution we will be using the following formulae;
$hy{p^2} = op{p^2} + ad{j^2}$ where $hyp$ signifies hypotenuse side of a right angled triangle, $opp$ is opposite side, and $adj$ is the adjacent side.

Complete Step-by-Step solution:

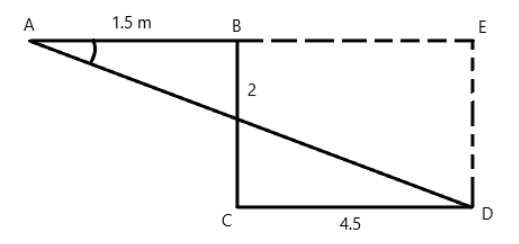
As shown in the diagram above, man travels east (which is rightward) $1.5$ m, then he travels south 9which is downward) 2 m, and finally east again by $4.5$ m.
To calculate the total distance travelled, we simply sum of the entire short distances. We do that as follows,
${d_t} = {d_{AB}} + {d_{BC}} + {d_{CD}}$which by insertion of given values will be
${d_t} = 1.5 + 2 + 4.5 = 8m$
Hence, the total distance covered is equal to 8 m.
Now to calculate the displacement, we draw a line from the beginning of the journey to the end, and calculate its length.
From the diagram, we can see that the triangle ADE is a right angled triangle, hence, we the line AD is which is the displacement is the hypotenuse of the triangle. Hence, from Pythagoras theorem
$hy{p^2} = op{p^2} + ad{j^2}$where$hyp$ signifies hypotenuse side of a right angled triangle, $opp$ is opposite side, and $adj$ is the adjacent side.
We have that the displacement $l$ can be calculated from
${l^2} = {\left( {1.5 + 4.5} \right)^2} + {2^2} = {6^2} + {2^2}$
$\Rightarrow {l^2} = 40$
Hence, by using square root, we have that
$\Rightarrow l = \sqrt {40} = 2\sqrt {10} m$
For the direction, we have that
$\tan \theta = \dfrac{{{d_{ED}}}}{{{d_{AE}}}} = \dfrac{2}{6}$
$\theta = {\tan ^{ - 1}}\left( {\dfrac{1}{3}} \right) = 18.4^\circ$

Hence, the direction is $18.4^\circ$ from the east towards the south.

Note: Note that, because displacement is a vector, it is imperative that when told to calculate it, the direction must be included unless where told otherwise. This is often a common mistake.