Solveeit Logo
Login

Question

Question: A man starts from O moves 500 m turns by \({{60}^{\circ }}\)and moves 500 m again turns by \({{60}^{...

A man starts from O moves 500 m turns by 60∘{{60}^{\circ }}and moves 500 m again turns by 60∘{{60}^{\circ }} and moves 500 m and so on. Find the displacement after (i) 5th{{5}^{th}} turn, (ii) 3rd{{3}^{rd}} turn?

Explanation

Solution

The entire path travelled by the man makes a hexagon. The displacement at the 5th and the 3rd turn can be calculated by the magnitude of resultant vector magnitude calculation. And as we know the resultant is the vector sum of two or more vectors. It is the result of adding two or more vectors together.

Complete step by step answer:

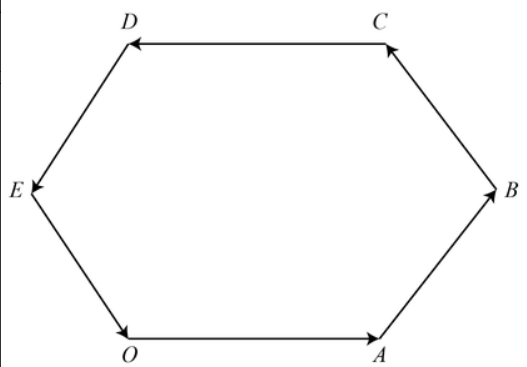
(i) 5th{{5}^{th}} turn
The displacement will be equal to the vector: OE→ \overset{\to }{\mathop{OE}}\, as shown in the figure.
Clearly, we can say that the displacement of 5th{{5}^{th}} turn is 500 m because the man moves at turns of 500 m.

(ii) 3rd{{3}^{rd}} turn
The displacement will be equal to the vector: OC→ \overset{\to }{\mathop{OC}}\, as shown in the figure.
We can say that:
OC→ =OA→ +AC→ \overset{\to }{\mathop{OC}}\,=\overset{\to }{\mathop{OA}}\,+\overset{\to }{\mathop{AC}}\,
So, ∣OC→ ∣=∣OA→ ∣2+∣AC→ ∣2+2∣OA→ ∣∣AC→ ∣cos⁡90∘\left| \overset{\to }{\mathop{OC}}\, \right|=\sqrt{{{\left| \overset{\to }{\mathop{OA}}\, \right|}^{2}}+{{\left| \overset{\to }{\mathop{AC}}\, \right|}^{2}}+2\left| \overset{\to }{\mathop{OA}}\, \right|\left| \overset{\to }{\mathop{AC}}\, \right|\cos {{90}^{\circ }}}
Also, AC→ =AB→ +BC→ \overset{\to }{\mathop{AC}}\,=\overset{\to }{\mathop{AB}}\,+\overset{\to }{\mathop{BC}}\,
So, ∣AC→ ∣=∣AB→ ∣2+∣BC→ ∣2+2∣AB→ ∣∣BC→ ∣cos⁡60∘\left| \overset{\to }{\mathop{AC}}\, \right|=\sqrt{{{\left| \overset{\to }{\mathop{AB}}\, \right|}^{2}}+{{\left| \overset{\to }{\mathop{BC}}\, \right|}^{2}}+2\left| \overset{\to }{\mathop{AB}}\, \right|\left| \overset{\to }{\mathop{BC}}\, \right|\cos {{60}^{\circ }}}
Since each turn is of 500m, so ∣AB→ ∣=∣BC→ ∣=∣OA→ ∣=500\left| \overset{\to }{\mathop{AB}}\, \right|=\left| \overset{\to }{\mathop{BC}}\, \right|=\left| \overset{\to }{\mathop{OA}}\, \right|=500
So,
∣AC→ ∣=(500)2+(500)2+2(500)(500)12 =5003m\begin{aligned} & \left| \overset{\to }{\mathop{AC}}\, \right|=\sqrt{{{\left( 500 \right)}^{2}}+{{\left( 500 \right)}^{2}}+2\left( 500 \right)\left( 500 \right)\dfrac{1}{2}} \\\ & =500\sqrt{3}m \end{aligned}
Now,
∣OC→ ∣=(500)2+(5003)2+2(500)(5003)(0) =1000m\begin{aligned} & \left| \overset{\to }{\mathop{OC}}\, \right|=\sqrt{{{\left( 500 \right)}^{2}}+{{\left( 500\sqrt{3} \right)}^{2}}+2\left( 500 \right)\left( 500\sqrt{3} \right)\left( 0 \right)} \\\ & =1000m \end{aligned}

Note:
In order to solve this question, remember to calculate the magnitude of a resultant vector. The displacement at the given turns are the resultant of vectors drawn from the tail and head of both vectors.