Question
Question: A man stands 9m away from a flag – pole. He observes that the angle of elevation of the top of the p...
A man stands 9m away from a flag – pole. He observes that the angle of elevation of the top of the pole is 28∘ and the depression of the bottom of the pole is 13∘ . Calculate the height of the pole.
Solution
Hint: To find the height of the pole first we need to draw the diagram to understand the data in question. Take AB as a pole where AB=AE+BE then find BE with the help of tan13∘ and AE with the help of tan28∘ . We can use the value of tan13∘=0.23086 and tan28∘=0.5317.
Complete step-by-step answer:
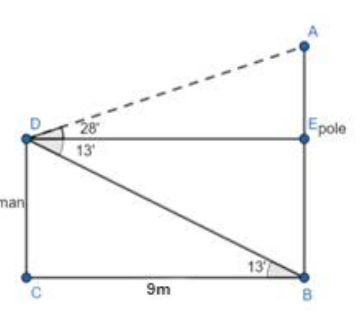
A man stands 9m away from a flag pole i.e. BC=DE=9m .
He observes that the angle of elevation of the top of the pole is 28∘ i.e. ∠ADE=28∘ and the angle of depression of the bottom of the pole is 13∘ i.e. ∠EDB=13∘ .
CD=BE.
In ΔBDE .
tanθ=DEBE .
tan13∘=9BE ( Here DE=9cm) .
0.23086=9BE ( Here tan13∘=0.23086).
Now, multiply both side by ′9′ we get –
0.23056×9=BE2.077=BE.
In ΔADE
tanθ=DEAE .
tan28∘=9AE ( where DE=9m ).
0.53.17=9AE ( HERE tanθ=0.5317 ).
Multiplying both side by ′9′ we get –
0.5317×9=AE4.785=AE
Height of the pole =AE+BE
=4.785+2.077
=6.862m.
Hence the height of the pole is 6.862m.
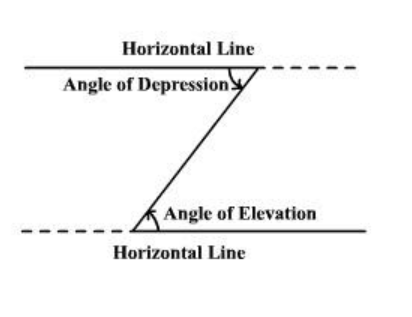
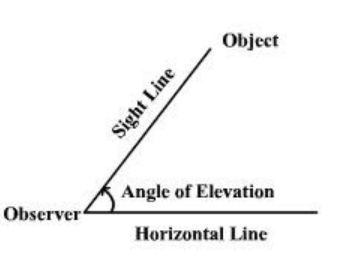
Note: In this question students may get confused because of angle of elevation and angle of depression. They should know the difference between angle of elevation and angle of depression. The term angle of elevation denotes the angle between the horizontal upward to an object.
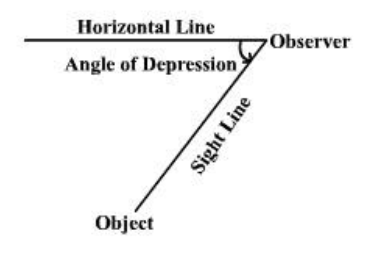
The term of depression denotes the angle from the horizontal down was to an object.
The angle of elevation and the angle of depression are congruent.