Question

A man standing on a platform finds that a train takes 3 seconds to pass him and another train of the same length moving in the opposite direction takes 4 seconds. The time taken by the trains to pass each other will be
(A) $2\dfrac{3}{7}$ sec
(B) $3\dfrac{3}{7}$ sec
(C) $4\dfrac{3}{7}$ sec
(D) $5\dfrac{3}{7}$ sec

Answer 1

Hint: Assume that the length of train A and train B be x meters. To pass the man who is standing on the platform, train A and train B has to cover the same distance as of its length. It means both trains need to cover the distance x to pass the man who is standing on the platform. Train A takes 3 seconds to pass him and another train of the same length moving in the opposite direction takes 4 seconds. We know the formula, $\text{Speed=}\dfrac{\text{Distance}}{\text{Time}}$ . Use this formula and get the speed of train A and train B. Now, both trains are running towards each other. The relative distance to be covered by the trains is 2x. We know that when two objects are approaching each other then their relative speed is given by the summation of the individual speed of the objects. Therefore, the relative speed of the train is $\left( \dfrac{x}{3}+\dfrac{x}{4} \right)m/s$ . Now, use the formula $\text{Time=}\dfrac{\text{Relative }\text{distance}}{\text{Relative speed}}$ and calculate the time.

Complete step-by-step answer:
According to the question, it is given that we have two trains A and B. A man standing on a platform finds that train A takes 3 seconds to pass him and another train B of the same length moving in the opposite direction takes 4 seconds.
First of all, let us assume that the length of train A and train B be x meters ………………….(1)
To pass the man who is standing on the platform, train A has to cover the same distance as of its length, and from equation (1), we have the length of train A.
The time taken by train A to cross the man standing on the platform = 3 seconds …………………………….(2)
Distance to be covered = x meters …………………..(3)
We know the formula, $\text{Speed=}\dfrac{\text{Distance}}{\text{Time}}$ …………………….(4)
Now, putting the values of time from equation (2) and distance from equation (3), in the formula shown in equation (4), we get
Speed of train A = $\dfrac{x}{3}m/s$ ………………………………(5)
Now, to the man who is standing on the platform, train B has to cover the same distance as of its length, and from equation (1), we have the length of train B.
The time taken by train B to cross the man standing on the platform = 4 seconds …………………………….(6)
Distance to be covered = x meters …………………..(7)
Now, putting the values of time from equation (6) and distance from equation (7), in the formula shown in equation (4), we get
Speed of train B = $\dfrac{x}{4}m/s$ ……………………………..(8)
Now, train A and train B are running in the opposite direction to pass each other.

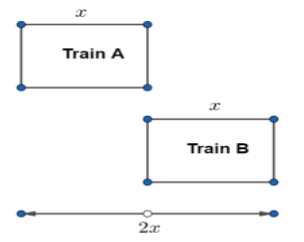
We can see that this is a case of relative motion. From the figure, we can see that the trains have to cover the distance 2x to pass each other completely.
Relative distance to be covered by train A and train B = 2x meters……………………….(9)
We know that when two objects approach towards each other then their relative speed is given by the summation of the individual speed of the objects.
From equation (5) and equation (8), we have the speed of train A and train B.
Here, we have, the speed of train A is $\dfrac{x}{3}m/s$ and the speed of train B is $\dfrac{x}{4}m/s$ .
So, the relative speed of train A and train B = $\dfrac{x}{3}+\dfrac{x}{4}m/s$ …………………………(10)
We know the formula, $\text{Time=}\dfrac{\text{Relative }\text{distance}}{\text{Relative speed}}$ …………………………(11)
Now, putting the values of relative distance from equation (9) and relative speed from equation (10), in the formula shown in equation (11), we get
$\text{Time=}\dfrac{2x}{\dfrac{x}{3}+\dfrac{x}{4}}=\dfrac{2x}{\dfrac{4x+3x}{12}}=\dfrac{2x\times 12}{7x}=\dfrac{24}{7}=3\dfrac{3}{7}\sec$ .
Therefore, the time taken by the trains to pass each other is $3\dfrac{3}{7}$ sec.

Note: In this question, one might calculate the relative speed as $\left( \dfrac{x}{3}-\dfrac{x}{4} \right)m/s$ . This is wrong because train A and train B are approaching each other and we know that when two objects approach towards each other then their relative speed is given by the summation of the individual speed of the objects. Therefore, the relative speed of the train is $\left( \dfrac{x}{3}+\dfrac{x}{4} \right)m/s$ .