Question

A man sits on a chair supported by a rope passing over a frictionless fixed pulley. The man who weighs $1000N$ exerts a force of $450N$ on the chair downwards while pulling on the other end of the rope. If the chair weighs $250N$ and $g$ is $10m/{{s}^{2}}$ , then the acceleration of the chair is,
A. $0.45m/{{s}^{2}}$
B. $0m/{{s}^{2}}$
C. $2m/{{s}^{2}}$
D. $\left( 9/25 \right)m/{{s}^{2}}$

Answer 1

Hint: This problem can be solved by properly considering all the forces on each object, that is, the chair and the human as a system first and then individually, and applying Newton’s second law of motion which states that the force exerted by or on a body is the product of the mass of the body and the acceleration of the body in the direction of the force due to it. The acceleration of the chair and the human will be equal in magnitude since the man is sitting on the chair and they can be considered as a system.

Formula used:
$F=ma$ (Newton’s second law) where $F$ is the force applied on a body of mass $m$ and $a$ is the acceleration of the body due to that force.
$W=Mg$ where $W$ is the weight of the body, $M$ is its mass and $g$ is the acceleration due to gravity.
According to Newton’s third law of motion, when object 1 applies a force ${{F}_{12}}$ on another object 2, then an equal and opposite force ${{F}_{21}}$ is applied by the second object on the first.
${{F}_{12}}=-{{F}_{21}}$ (Newton’s third law)

Complete step by step answer:
Let us first draw a diagram to understand the problem better.

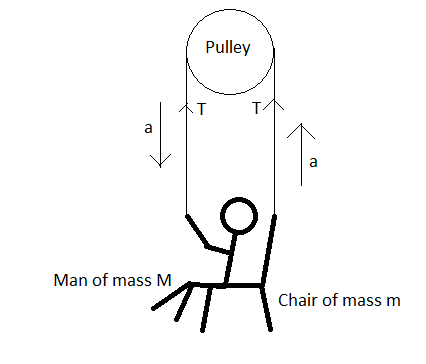
Let the mass of the man be $M$ and the mass of the chair be $m$. The tension in the rope is $T$. Let the part of the rope connected with the chair move upwards with an acceleration $a$. Since, the rope is inextensible the other part of the rope held by the man will move downward with the same acceleration $a$. However, the man and the chair will up together with an acceleration $a$. Acceleration due to gravity $g=10m/{{s}^{2}}$
$W=Mg$ --(1) where $W$ is the weight of the body, $M$ is its mass and $g$ is the acceleration due to gravity.
Given weight of the man is ${{W}_{man}}=1000N$ Hence, using (1), we get the mass of the man as $M=\dfrac{{{W}_{man}}}{g}=\dfrac{1000}{10}=100kg$
Given weight of the man is ${{W}_{chair}}=1000N$ Hence, using (1), we get the mass of the chair as $m=\dfrac{{{W}_{chair}}}{g}=\dfrac{250}{10}=25kg$
The normal force exerted by the person on the chair downwards is $\left( N \right)=450N$. According to Newton’s third law of motion, when object 1 applies a force ${{F}_{12}}$ on another object 2, then an equal and opposite force ${{F}_{21}}$ is applied by the second object on the first.
${{F}_{12}}=-{{F}_{21}}$ (Newton’s third law)
Therefore, the chair exerts a normal force upward on the human equal to $\left( N \right)=450N$.
Now, let us draw the free body diagram (FBD) of the man-chair system.

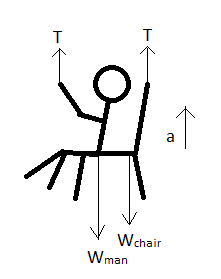
The system moves up with an acceleration $a$. Now, $F=ma$ (Newton’s second law) --(2) where $F$ is the force applied on a body of mass $m$ and $a$ is the acceleration of the body due to that force.
Applying (2) in the FBD of the man-chair system we get,
$T+T-{{W}_{chair}}-{{W}_{man}}=\left( M+m \right)a$ $\therefore 2T-1000-250=\left( 100+25 \right)a=125a$ $\therefore 2T-1250=125a$ $\therefore T=\dfrac{125a+1250}{2}$ --(3)
Now, let us draw the FBD of the chair. 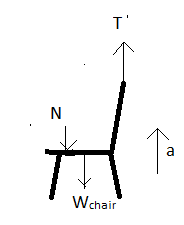Applying (2) in the FBD of the chair we get, $T-N-{{W}_{chair}}=ma$ $\therefore T-450-250=25a$ $\therefore T-700=25a$ Using (3), we get, $\dfrac{125a+1250}{2}-700=25a$ $\therefore 125a+1250-1400=50a$ $\therefore 125a-50a=1400-1250$ $\therefore 75a=150$ $\therefore a=\dfrac{150}{75}=2m/{{s}^{2}}$
Hence, the acceleration of the chair is $2m/{{s}^{2}}$ in the upward direction. Hence, the correct answer is C) $2m/{{s}^{2}}$.

Note: This problem could also have been solved by taking the free body diagram of the man instead of the chair and applying (2) and it would yield the same result. In this problem, it is very common that students cannot understand that the man and the chair will move together with the same acceleration. They think that since they are connected to different ends of the rope, one will have a downward acceleration, while the other will have an upward acceleration. Thus, they mark the directions of the acceleration wrong and arrive at a completely wrong answer.