Question

A man runs across the roof-top of a tall building and jumps horizontally to land on the roof of the next building which is at a lower height than the first. If his speed is$9m{s^{ - 1}}$, the horizontal distance between the two buildings is $10m$ and height difference is$9m$, will he be able to land on the next building? $\left( {g = 10m{s^{ - 2}}} \right)$

Answer 1

We are first going to draw a figure for the information given in the question, then, taking up the horizontal and the vertical motions for the man, we will calculate the time of flight for vertical motion, and then, the horizontal distance covered, which tells us whether he will be able to land or not.

Formula used: The equation of motion is given by
$y = ut + \dfrac{1}{2}a{t^2}$
Where, $y$is the distance covered, $u$is initially speed and $t$is time taken.

Complete step by step solution:
Let us first construct a figure for the given situation

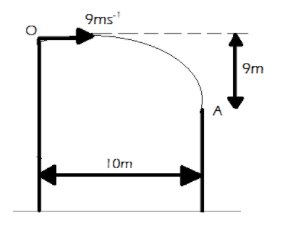
The man’s speed is given as $9m{s^{ - 1}}$
The horizontal distance between the buildings is$10m$and the height difference is$9m$
Let the time taken for the man to fall from points $O$to $A$be $t\,$seconds.
Taking the vertical downward motion from $O$to$A$, we get
{y_0} = 0 \\\ y = 9m \\\ {u_y} = 0 \\\ {a_y} = 10m{s^{ - 2}} \\\

We need to find time, $t\,$
The equation of motion is
${y_0} = y = {u_y}t + \dfrac{1}{2}{a_y}{t^2}$
Putting the values in this, we get
$- 9 = 0 \times t + \dfrac{1}{2} \times \left( { - 10} \right) \times {t^2}$
Finding the value of$t\,$, we get
$t = \sqrt {\dfrac{{9 \times 2}}{{10}}} = \sqrt {1.8} s$
Now, considering the horizontal direction of motion,
${v_x} = 9m{s^{ - 1}}$
If $R$is the horizontal distance travelled,
$R = {v_x}t$
Putting the values in this,

R = 9 \times \sqrt {1.8} \\\ \Rightarrow R = 12m \\\

Thus, the man will be able to land on the building.

Note: It is important to note that the charged particles can be created or destroyed as long as the net charge on the particles before and after the process remains the same. But in that case also, charge is not being created but the charged particles only transfer charge from one system to another.