Question

A man running a race course notes that the sum of the distances from the two flag posts from him is always 10 m and the distance between flag posts is 8m. The equations of the path traced by the man is given by
A.$\dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{{25}} = 1$
B.$\dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{{16}} = 1$
C.$\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1$
D.$\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{25}} = 1$

Answer 1

Here, we have to find out the equations of the path traced by the man. From the given equations, in the option, we can say that the pat must be an ellipse. First, we will trace the shape of the path. Then we will find the length of the major axis and the length of the minor axis using the focal length and distance between foci. Then we will substitute in the equation of the ellipse to find the equation of the path traced by the man.

Formula used:
We will use the formula of the distance between the foci is given by ${c^2} = {a^2} - {b^2}$ where $a$ and $b$ is the length of the major axis and minor axis respectively.

Complete step-by-step answer:
Let $S$ and $S'$ be two flag posts. The sum of the distance of man P from $S$ and $S'$ is equal to 10m.
Since the sum of distance of a point from any two fixed points $S$ and $S'$ in the plane is constant, it forms an ellipse
So, the equation of posts traced by the man is the same as an ellipse equation.

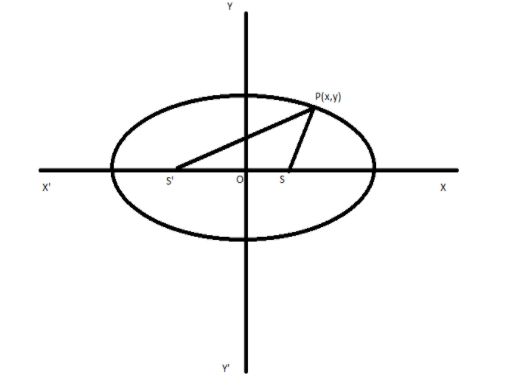
Let the equation of the ellipse be, $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$.
So, $S$ and $S'$ are the foci of the ellipse. x-axis is the major axis, y-axis is the minor axis.
We are given that the sum of the distance of man P from $S$ and $S'$is $10$m. Therefore,
Sum of distance of a point from foci$= 10m$
$\Rightarrow 2a = 10$
Dividing by 2 on both the sides, we have
$\Rightarrow a = \dfrac{{10}}{2}$
$\Rightarrow a = 5m$
Also, it is given that Distance between flag posts $SS'$ is 8 m.
$\Rightarrow$Distance between two foci $= 8m$
$\Rightarrow 2c = 8$
Dividing by 2 on both the sides, we have
$\Rightarrow c = \dfrac{8}{2}$
$\Rightarrow c = 4m$
Now, by using the formula ${c^2} = {a^2} - {b^2}$, we get
$\Rightarrow b = \sqrt {{a^2} - {c^2}}$
Substituting the values of $a = 5m$ and $c = 4m$, we have
$\Rightarrow b = \sqrt {{5^2} - {4^2}}$
$\Rightarrow b = \sqrt {25 - 16}$
$\Rightarrow b = \sqrt 9$
$\Rightarrow b = 3$
The equation of the ellipse is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$
Substituting the values of $a = 5m$ and $b = 3m$, we have
$\Rightarrow \dfrac{{{x^2}}}{{{5^2}}} + \dfrac{{{y^2}}}{{{3^2}}} = 1$
$\Rightarrow \dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1$
Therefore the required equation is $\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1$.

Note: An ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. The set of all points in a plane, the sum of whose distances from two fixed points in the plane is constant is an ellipse. These two fixed points are the foci of the ellipse. When a line segment is drawn joining the two focus points, then the mid-point of this line is the center of the ellipse. This line joining the two foci is called the major axis and a line drawn through the center and perpendicular to the major axis is the minor axis. The endpoints of the major axis are called vertices of the ellipse.