Question
Question: A man pulls himself up the 30\(^{\circ }\) incline by the method shown in Fig. If the combined mass ...
A man pulls himself up the 30∘ incline by the method shown in Fig. If the combined mass of the man and the cart is 100kg, determine the acceleration of the cart if the man exerts a pull of 250N on the rope. Neglect all friction and the mass of the rope, oulleysand wheels: (Given g=10ms−2)
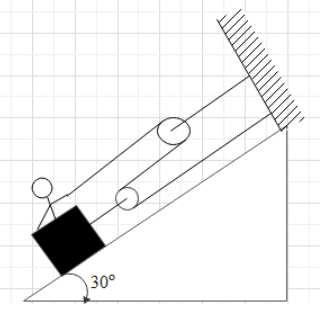
A. 4.5ms−2
B. 2.5ms−2
C. 3.5ms−2
D. 1.5ms−2
Solution
Find the net tension force acting on the system of the man and the cart. Then calculate the other forces acting on the system. Divide the gravitational force into two components, one parallel to the inclined plane and the other perpendicular to the plane. Then calculate the net force on the system. Then use Newton’s second law and find the acceleration of the system.
Formula used:
F=mg
Fnet=ma
Complete answer:
When the man pulls the rope with a force of 250N, a tension will develop in the rope equal to the force applied on it. Let the tension in the rope be T. Therefore, T = 250N.
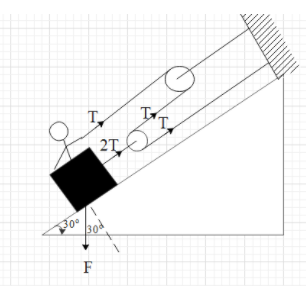
As we can see that the rope is attached to the cart with means of a pulley. Due to this a tension equal to 2T will develop in the rope attached to the cart.
Hence, the net tension force acting in the combined mass of the man and the cart is 2T+T = 3T.
Now, let us find the other forces acting on the system of the man and the cart. The gravitational force will act on the system in the downward direction.
The gravitational force is given as F = mg, where m is the mass of the system and g is acceleration due to gravity.
Hence, F = (100)(10) = 1000N.
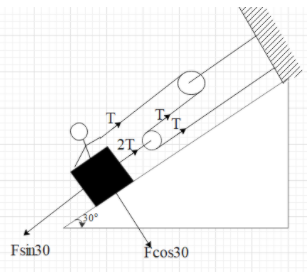
Now resolve the gravitational force F into two components. One along the inclined plane (equal to Sin 30) and the other in perpendicular to the plane of inclination (equal to Cos 30), as shown.
The perpendicular component will be balanced by the normal force exerted by the plane.
The force Fsin30 will be in the opposite direction to the direction of the tension.
Therefore, the net force on the system is Fnet=3T−Fsin30.
⇒Fnet=3T−2F.
Substitute the values of F and T.
⇒Fnet=3(250)−21000=750−500=250N.
From Newton’s second law motion we know that Fnet=ma, where a is the acceleration of the system.
⇒a=mFnet.
⇒a=mFnet=100250=2.5ms−2
This means that acceleration of the body is 2.5ms−2.
Hence, the correct option is B.
Note:
The system of the man and the cart will move up the inclined plane only when the net tension force is greater than the component of the gravitational force parallel to the inclined plane.
Note that the acceleration of the cart and the man is the same and in the upwards direction parallel to the inclined plane.
