Question

A man places a rectangular glass slab of thickness $9cm$ on a newspaper. On the top of glass slab he placed a glass beaker of negligible wall thickness containing water up to a height of $6cm$ . if refractive index of glass is $1.5$ and refractive index of water is $\left( {\dfrac{4}{3}} \right)$ , what is the apparent depth of the newspaper?

Answer 1

We can solve this question in two parts first we take lower medium after refraction the image formed will work as an object for upper medium then we take upper medium and find the apparent depth due to this medium that will be the final apparent depth.

Complete step by step solution:
In diagram the arrangement shown

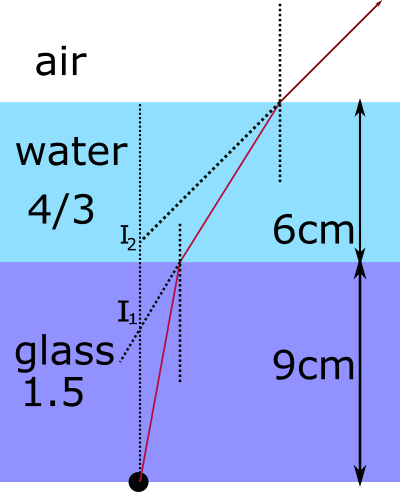
Step 1
First we take refraction from glass slab when see from water then apparent depth from upper end of glass slab can be calculated as
We know the apparent depth given by $AD = \dfrac{d}{{_r{n_d}}}$
Where $_r{n_d}$ is the refractive index of denser medium with respect to rare medium
$\Rightarrow A{D_1} = \dfrac{9}{{_w{n_g}}}$
We know
$_w{n_g} = \dfrac{{_a{n_g}}}{{_a{n_w}}}$
So refractive index of glass with respect to water
$_w{n_g} = \dfrac{{\dfrac{3}{2}}}{{\dfrac{4}{3}}}$
$_w{n_g} = \dfrac{9}{8}$
So apparent depth
$\Rightarrow A{D_1} = \dfrac{9}{{\dfrac{9}{8}}}$
$A{D_1} = 8cm$
Image formed at $8cm$ below upper end of glass slab this work as image for water

Step 2
Now we take refraction from water air surface
For this the real depth = height of water + AD1
Real depth = $\left( {6 + 8} \right) = 14cm$
Apply formula for apparent depth
$\Rightarrow A{D_2} = \dfrac{{14}}{{_a{n_w}}}$
$\Rightarrow A{D_1} = \dfrac{{14}}{{\dfrac{4}{3}}}$
Solving this
$\Rightarrow A{D_2} = \dfrac{{21}}{2}cm$ from upper end of water surface
So the apparent depth due to system of both medium is $\left( {\dfrac{{21}}{2}} \right)cm$ when see from air

So the apparent depth of newspaper is $\left( {\dfrac{{21}}{2}} \right)cm.$

Note: By this method we can solve these types of questions we can also solve this question by another method:
We have direct formula for apparent depth if refractive index of medium ${n_1},{n_2}$ with respect to air and depth of medium is ${d_1},{d_2}$ then
$\Rightarrow AD = \dfrac{{{d_1}}}{{{n_1}}} + \dfrac{{{d_2}}}{{{n_2}}}$
$\Rightarrow AD = \dfrac{9}{{\dfrac{3}{2}}} + \dfrac{6}{{\dfrac{4}{3}}}$
Solving this
\Rightarrow AD = 6 + \dfrac{9}{2} \\\ AD = \dfrac{{21}}{2}cm \\\