Question

A man on the top of a vertical tower observes a car moving at a uniform speed towards the tower on a horizontal road. If it takes $18$min. for the angle of depression of the car change from $30^\circ$ to $45^\circ$; then after this, the time taken(in min.) by the car to reach the foot of the tower ,is?
(A) $9\left( {1 + \sqrt 3 } \right)$
(B) $\dfrac{9}{2}\left( {\sqrt 3 - 1} \right)$
(C) $18\left( {1 + \sqrt 3 } \right)$
(D) $18\left( {\sqrt 3 - 1} \right)$

Answer 1

The angle of depression of car changes from $30^\circ$ to $45^\circ$. It means the car moves in the direction of the tower. Consider the two triangles differently and then form relations for both the triangles. Later solve the relations to get the desired answer.

Complete step-by-step answer:
Consider the following figure.

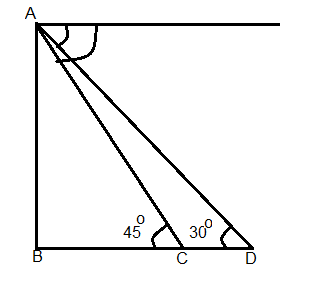
Let $A$ be the position of the man and $AB$ be the tower.
Now consider the triangle$ABD$.
$\tan 30^\circ = \dfrac{{AB}}{{BD}}$
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{AB}}{{BC + CD}}$
$\Rightarrow \dfrac{{BC + CD}}{{\sqrt 3 }} = AB$ …………...…. (1)
Now consider the triangle $ABC$.
$\tan 45^\circ = \dfrac{{AB}}{{BC}}$
$\Rightarrow 1 = \dfrac{{AB}}{{BC}}$
$\Rightarrow BC = AB$ …………….….(2)
Substitute the value of $BC$ from equation (2) in equation (1), we have
$\dfrac{{AB + CD}}{{\sqrt 3 }} = AB$
$\Rightarrow AB + CD = \sqrt 3 AB$
$\Rightarrow \sqrt 3 AB - AB = CD$
$\Rightarrow AB\left( {\sqrt 3 - 1} \right) = CD$ ……………...…. (3)
Let $v$ m/min be the speed of the car.
Since the car takes $18$min. to cover the distance$CD$, we have
$CD = 18v$ …………..…. (4) $\left[ {Dis\tan ce = Speed \times Time} \right]$
Substitute the value of $CD$ from equation (4) in equation (3), we have
$AB\left( {\sqrt 3 - 1} \right) = 18v$
$\dfrac{{AB\left( {\sqrt 3 - 1} \right)}}{{18}} = v$ …………...…. (5)
We need to find the time taken by the car to cover the distance $BC$.
$Time = \dfrac{{BC}}{v}$ $\left[ {Time = \dfrac{{Dis\tan ce}}{{Speed}}} \right]$
$\Rightarrow Time = \dfrac{{18BC}}{{AB\left( {\sqrt 3 - 1} \right)}}$ [from equation (5)]
$\Rightarrow Time = \dfrac{{18AB}}{{AB\left( {\sqrt 3 - 1} \right)}}$ [from equation (2)]
$\Rightarrow Time = \dfrac{{18}}{{\left( {\sqrt 3 - 1} \right)}}$
$\Rightarrow Time = \dfrac{{18}}{{\left( {\sqrt 3 - 1} \right)}} \times \dfrac{{\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 + 1} \right)}}$
$\Rightarrow Time = \dfrac{{18\left( {\sqrt 3 + 1} \right)}}{{3 - 1}}$
$\Rightarrow Time = \dfrac{{18\left( {\sqrt 3 + 1} \right)}}{2}$
$\Rightarrow Time = 9\left( {\sqrt 3 + 1} \right)$

Hence option (A) is the correct answer.

Note: The distance travelled by the car moving through velocity $v$ in $t$ seconds is given by : $x = v \times t$.
For a constant distance, speed and time are inversely proportional. With increase in speed time decreases and with decrease in speed, time increases.