Solveeit Logo
Login

Question

Question: A man on the top of a vertical tower observes a car moving at a uniform speed coming directly toward...

A man on the top of a vertical tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change its measure from 30 to 45, how soon after this will the car reach the tower?

Explanation

Solution

Hint : “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”, this is the Pythagoras theorem. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle 90∘.90^\circ .
Approaching by diagram use of Pythagoras theorem: H2=B2+P2{H^2} = {B^2} + {P^2}
SubstitutingH=LH = L,B=AB = Aand P=KP = K, we have:

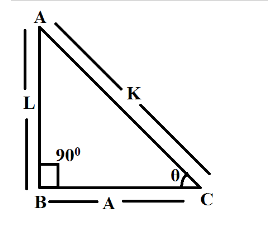
L2+A2=K2{L^2} + {A^2} = {K^2} and by trigonometric ratios:
sin⁡θ=LK\sin \theta = \dfrac{L}{K}; cos⁡θ=AK\cos \theta = \dfrac{A}{K}; tan⁡θ=LK\tan \theta = \dfrac{L}{K}

Complete step-by-step answer :
Let the height of the tower be h
Angles of depression of moving cars with respect to man changes from 30∘{30^ \circ }to45∘{45^ \circ }.

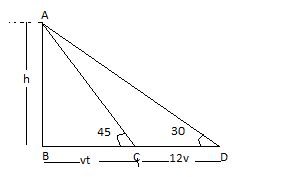
We know
Distance = Speed x time
This can be written as
Distance =v×t=vt = v \times t = vt
Now in △ABC\vartriangle ABC

\tan {45^ \circ } = \dfrac{{AB}}{{BC}} \\\ 1 = \dfrac{h}{{vt}} \\\ vt = h - - (i) \\\ $$[Since$$\tan {45^ \circ } = 1$$] Now in$$\vartriangle ABD$$

\tan {30^ \circ } = \dfrac{{AB}}{{BD}} \\
\tan {30^ \circ } = \dfrac{h}{{vt + 12v}} \\

HencebysolvingHence by solving

\tan {30^ \circ } = \dfrac{h}{{vt + 12v}} \\
\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{vt + 12v}} \\
vt + 12v = \sqrt {30} h \\

Since $$vt = h$$from equation (i), we can write

vt + 12v = \sqrt 3 h \\
vt + 12v = \sqrt 3 vt \\
\sqrt 3 vt - vt = 12v \\
vt\left( {\sqrt 3 - 1} \right) = 12v \\
\left( {\sqrt 3 - 1} \right) = \dfrac{{12v}}{{vt}} \\
\left( {\sqrt 3 - 1} \right) = \dfrac{{12}}{t} \\

Hencebysolving,wegetHence by solving, we get

1.732 - 1 = \dfrac{{12}}{t} \\
0.732 = \dfrac{{12}}{t} \\
t = \dfrac{{12}}{{0.732}} \\

HencethetimeistakenbythecartillitreachesthetowerHence the time is taken by the car till it reaches the tower

t = \dfrac{{12}}{{0.732}} \\
= \dfrac{{1200}}{{732}} \\
= 16.43\min \\

∗∗Note∗∗:Studentsshouldnotbeconfusedwiththeangleofelevationandtheangleofdepression.Thesearetwodifferentthings.Theangleofelevationistherisinganglegenerally,fromthefootwhiletheangleofdepressionismeasuredforthetopofthetower. **Note** : Students should not be confused with the angle of elevation and the angle of depression. These are two different things. The angle of elevation is the rising angle generally, from the foot while the angle of depression is measured for the top of the tower.