Question

A man on the deck of a ship is $12m$ above water level. He observes that the angle of elevation of the top of a cliff is ${45^ \circ }$ and the angle of depression of its base is ${30^ \circ }$ . Calculate the distance off the cliff from the ship and the height of the cliff.
A. Height $= 36m,$ Distance $= 29m$
B. Height $= 46.256m,$ Distance $= 13.759m$
C. Height $= 40m,$ Distance $= 25m$
D. Height $= 32.784m,$ Distance $= 20.784m$

Answer 1

Hint : As we know that the above given question is a word problem. A problem is a mathematical question written as one sentence or more describing a real life scenario where that problem needs to be solved by the way of mathematical calculation. We can solve the given problem by applying trigonometric ratios formulas.

Complete step-by-step answer :
As per the given question we have to find the distance off the clip and the height off the cliff. Let us first draw the diagram according the question,

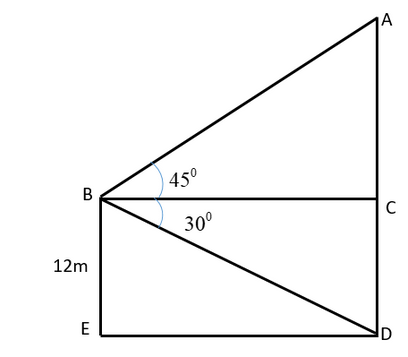
Now according to the question we can say that A man standing on the deck of a ship is $12m$ above water level i.e. $BE = DC = 12m$ and we have been given that the angle of elevation of the top of a cliff is $45$ degree i.e. $\angle ABC = {45^ \circ }$ and the angle of depression of the base of the cliff is $30$ degree i.e. $\angle DBC = {45^ \circ }$
According to the diagram we can say that Height of the cliff $= AD$ and The distance of the cliff from the ship = $BC$ .
Now in In ΔABC,
$\tan \theta = \dfrac{{perpendicular}}{{base}}$ .
We will now put the values and we have:
$\tan {45^ \circ } = \dfrac{{AC}}{{BC}} \\\ \Rightarrow 1 = \dfrac{{AC}}{{BC}}$ .
So we have $AC = BC$ .
Again in the triangle BCD, we have perpendicular $= DC$ and Base is $BC$ .
Therefore ,
$\tan 30 = \dfrac{{DC}}{{BC}}\\\ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{12}}{{BC}}$ .
Therefore the value of $BC = 12\sqrt 3 = 12 \times 1.732$ .
It gives $BC = 20.784$ . And we know that $BC = AC = 20.784$ , i.e. the distance off the cliff.
So Height of cliff $= AD = AC + BC$ , by putting values we have $20.784 + 12 = 32.784$ .
So the distance of the cliff from the ship is $20.784m$ and Height of the cliff is
$32.784m$ .
Hence the correct option is D. Height $= 32.784m,$ Distance $= 20.784m$ .
So, the correct answer is “Option D”.

Note : We should always be careful what the question is asking and we will find it in trigonometric terms. Based on the requirement and by observing all the necessary information that is already available in the question we gather the information and then create an equation or by unitary method whichever is applicable, then we solve the problem and then verify the answer by putting the value in the problem and see whether we get the same answer or not.