Question

A man on a cliff observes a boat at an angle of depression of $30^\circ$ which is approaching the shore to the point immediately beneath the observer with a uniform speed. Six minutes later, the angle of depression of the boat is found to be $60^\circ$ . Find the total time taken by the boat to reach the shore.

Answer 1

First express the environment of the problem through a figure and then assume the speed of the boat as $v$m/min and then apply the trigonometric ratio to get the relation between the height of the cliff and the distance covered by the boat and then use then to find the desired result.

Complete step by step solution:
We have given that a man on a cliff observes a boat at an angle of depression of $30^\circ$ which is approaching the shore to the point immediately beneath the observer with a uniform speed. Six minutes later, the angle of depression of the boat is found to be $60^\circ$.
The goal is to find the total time taken by the boat to reach the shore.
First assume the two positions of the boat at the two instants are $A$ and $D$, and let that the speed of the boat is $v$m/min, $h$ is the height of the cliff and $C$ is the location of the man. Then the figure is given as:

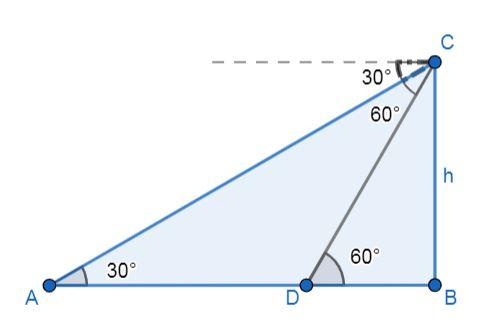
It is given in the problem that the time taken by the boat to the reach from the point $A$ to the point $D$ is $6$ min and the speed of the boat is $v$m/min, then the distance covered from the point $A$ to the point $D$ is given as:
${\text{Distance}} = {\text{Speed}} \times {\text{Time}}$
Distance AD$= 6v$

Now, assume that the boat takes $t$ time to reach the shore then the distance covered from the point $D$ to the point $B$ is given as:
DB$= vt$

Now, apply the trigonometric ratio in the triangle $DBC$,
$\tan 60^\circ = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$
We know that for the triangle $DBC$, $BC$ is the perpendicular and $DB$ is the base whose lengths are $BC = h$and$DB = vt$, then we have
$\tan 60^\circ = \dfrac{{BC}}{{DB}}$
$\Rightarrow \sqrt 3 = \dfrac{h}{{vt}}$
$\Rightarrow h = vt\sqrt 3$ … (1)

Now, apply the trigonometric ratio in the triangle $ABC$,
$\tan 30^\circ = \dfrac{{{\text{Perpendicular}}}}{{Base}}$
We know that for the triangle $ABC$, $BC$ is the perpendicular and $AB$ is the base whose lengths are $BC = h$ and $AB = 6v + vt$, then we have
$\tan 30^\circ = \dfrac{{BC}}{{AB}}$
$\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{v\left( {6 + t} \right)}}$
$\Rightarrow h = \dfrac{{v\left( {6 + t} \right)}}{{\sqrt 3 }}$ … (1)

Compare the values $h$ from the equation (1) and equation (2),
$vt\sqrt 3 = \dfrac{{v\left( {6 + t} \right)}}{{\sqrt 3 }}$

Simplify the equation:
$t\sqrt 3 \times \sqrt 3 = 6 + t$
Solve the equation for the value of $t$.
$3t = 6 + t$
$\Rightarrow 3t - t = 6$
$\Rightarrow 2t = 6$
$\Rightarrow t = 3$minutes

Therefore, the boat will take 3 minutes to reach the shore.
As given that take 6 minute to reach the point D from the point A and we have find that the boat take 3 minute to reach the shore from the point D, os the total time taken is:

**Total time$= 6 + 3 = 9$ minute.

Therefore, the boat will take 9 minute to reach the shore.**

Note: If the speed of the boat is $v$m/min then after $6$ minutes the boat reaches from the point $A$ to the point $D$, then the distance covered by the boat is given as the product of the speed and the time taken. That is,
Distance from A to D$= v \times 6 = 6v$