Question
Question: A man of mass \[\text{2m}\] is pulling up a block of mass \[\text{m}\] with constant velocity. The a...
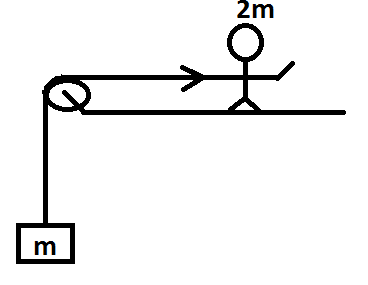
A man of mass 2m is pulling up a block of mass m with constant velocity. The acceleration of man is- (Neglect any friction)-
(A). g
(B). 2g
(C). 3g
(D). g/2
Solution
The figure has two separate systems and different forces are acting on each system. Resolve the systems. There are two main forces- tension in string and weight of block. Analyse each system and make equations. Solve the equations to find acceleration of man.
Formula used:
⇒ T = mg
mg = 2ma !!′!!
Complete step-by-step answer:
The block, pulley and man form an isolated system.
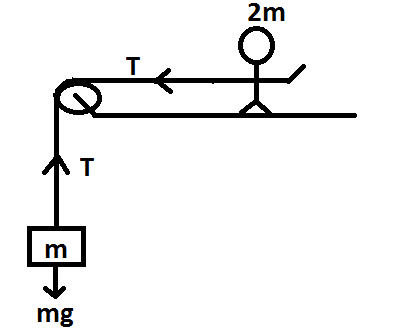
Let us divide the fig into two systems- the block and pulley system and the man and pulley system and consider the upward direction as (+) .
Forces acting on block and pulley system are- T and mg , where T is the tension in the string and mg is the weight acting on the block. The block is moving with uniform velocity in the upward direction which means there are no external forces acting on block, so,
a= 0 Here a is acceleration of block
Therefore-
T - mg = 0
⇒ T = mg - (1)
Force acting on the man pulley system is T and the system is moving opposite the direction of T with some acceleration. Therefore,
T = (2m)a !!′!! - (2)
2m is mass of man, a !!′!! is acceleration of man.
From eq (1) and eq (2), we get,
