Question
Question: A man of mass m on a platform of equal mass m and pulls himself by two ropes passing over pulleys as...
A man of mass m on a platform of equal mass m and pulls himself by two ropes passing over pulleys as shown in the figure. If he pulls each rope with a force equal to half his weight, his upward acceleration would be:
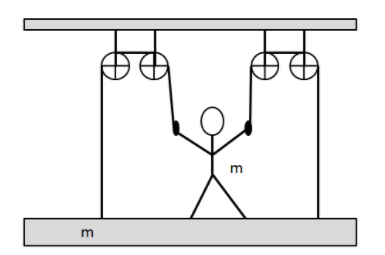
A.2g
B.4g
C.g
D.Zero
Solution
Hint: The figure given is that of pulley and platform arrangement. Hence, the prerequisites for solving this problem are knowledge of tension on ropes, how the tension gets distributed due to pulleys. Making a free body diagram will help further too. For this problem, the tension in each part of these ropes given by, T1=T2=T3=T4=2mg. If the net acceleration (a) of the plank and the body is a, then the summation of all the forces will give us the solution: i=1∑4Ti−Fdown=2ma.
Complete step-by-step answer:
Let’s start by making a free body diagram of the setup given.
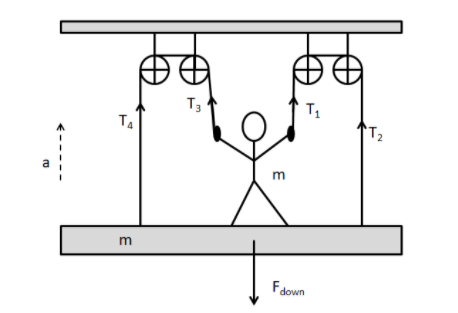
We have a man of mass (m) standing on a platform, which is of mass (m) as well. Hence the net downward force due to them is given by, Fdown=(m+m)g=2mg. A total of 4 pulleys are used here, with 2 on each side of the man. 2 long inextensible and massless ropes are used, which are connected to the platform as shown in the diagram. The man is pulling himself upward by pulling up the platform on which he stands with a net upward acceleration (a). Hence, the tension on each rope is as given in the diagram.
Given in the question is that, the man pulls each rope in his hand with force equal to half of his mass. Hence, T1=T3=2mg. Since the pulley isn’t connected to any other device, so there isn’t distribution of force seen over here. This implies, the tension acting on the rope, eventually connected to the platform are equal to, T2=T4=2mg.
Hence, the summation of all the forces is equal to the upward force generated due to pulling the platform with the man in it.
That is, i=1∑4Ti−Fdown=2ma.
Therefore, 2mg+2mg+2mg+2mg−2mg=2ma⇒2mg−2mg=2ma⇒2ma=0.
Hence, the net upward acceleration (a) is zero, since the mass can’t be zero.
Note: All the tension forces on the ropes are upward since the tension is similar to the Normal force acting on a body which acts against the force acting. Here the force acting is the mass of the man and the platform’s mass acting downward. Hence, the normal acts in the opposite direction, which is upward.
