Question
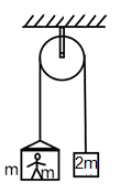
Question: A man of mass m is standing in a lift of the same mass m which is balanced on a pulley by a block of...
A man of mass m is standing in a lift of the same mass m which is balanced on a pulley by a block of mass 2m. If the man jumps suddenly with a velocity v0 upwards with respect to ground, then the speed of the man relative to lift just after he jumps would be
A v0
B 3v0
C 32v0
D 34v0
Solution
We assume the man lift and the block of mass 2 kg to be a system. Since the net external force on the system is zero therefore the momentum of the system will remain conserved. Initially the system is balanced and therefore the net velocity of the overall system is considered to be zero. Equating the initial momentum with the final momentum we get the velocity of the lift upwards. Velocity of the man with respect to the lift is the difference between the actual velocity of the man and actual velocity of the left.
Complete step by step answer:
We assume the man lifts and the block to be a system.The net external force on the system is zero and therefore conservation of momentum can be applied. Initially the system is at rest therefore the initial momentum of the system can be written as Pi=0.Let the final velocity of the left and so the block will be equal to v. The final velocity of the man is v0. Applying conservation of momentum,
Pi=Pf ⇒0=mv0−(m+2m)v ⇒mv0=3mv ⇒v=3v0
We know that the relative velocity of the man with respect to the lift (vman,lift) is given as the difference between the actual velocity of the man(vm=v0) and the actual velocity of the lift (vl=−3v0).
Therefore the velocity of the man with respect to the lift is,
vman,lift=vm−vl ⇒vman,lift=v0−(−3v0) ⇒vman,lift=v0+3v0 ∴vman,lift=34v0
Note: Students should not get confused between actual velocity and relative velocity. We should know the essential condition for the application of conservation of momentum that is when there is no external force on the system.Also, when the observer is also in motion, then we have to use the concept of relative velocity. We have to be particularly aware of the direction of the velocity as it is a vector quantity.
